Zadanie 2.3.2.2
Informacja
Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
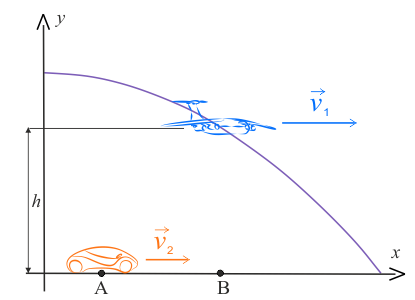
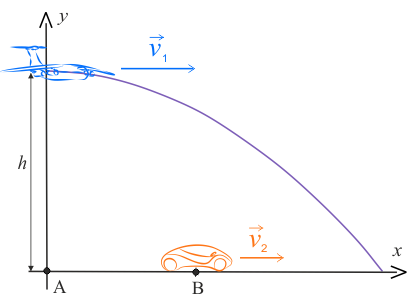
- prędkość, z jaką leci samolot oraz prędkość paczki \(\displaystyle{v_1=100\,\mathrm{\frac{m}{s}}}\),
- wysokość, na jakiej znajdował się samolot podczas zrzutu \(h=200\,\mathrm{m}\),
- odległość, między punktem, w którym znajdował się samolot podczas zrzutu, a położeniem w tym czasie samochodu \(\left | AB \right |=525\,\mathrm{m}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- prędkość, z jaką jedzie samochód \(v_2\).
Odpowiedź
Prędkość samochodu wynosiła \(\displaystyle{v_2=17\,\mathrm{\frac{m}{s}}}\).
Polecenie
Poniżej przedstawione są dwa rysunki. Który z nich przedstawia sytuację opisana w treści zadania?
Polecenie
Wskaż, spośród dwóch, jeden zestaw równań opisujących ruch samolotu i samochodu.
Równania dla paczki
\(\left\{\begin{matrix} x_1= &v_1t\\ y_1= &\frac{gt^2}{2} \end{matrix}\right.\)
Równania dla samochodu
\(\left\{\begin{matrix} x_2= &\left | AB \right | +v_2t\\ y_2= &v_2t \end{matrix}\right.\)
Równania dla paczki
\(\left\{\begin{matrix} x_1= &v_1t\\ y_1= &h-\frac{gt^2}{2} \end{matrix}\right.\)
Równania dla samochodu
\(\left\{\begin{matrix} x_2= &\left | AB \right | +v_2t\\ y_2= &0 \end{matrix}\right.\)
Rozwiązanie
Ruch paczki opisują równania rzutu poziomego. Rzut poziomy traktować możemy jako złożenie spadku swobodnego z wysokości \(h\) oraz ruchu poziomego ze stałą prędkością \(v_0=v_1\).
Równania dla paczki
Samochód porusza się po drodze, więc składowa pionowa ruchu jest równa zeru. Składową poziomą opisuje równanie ruchu jednostajnego.
Równania dla samochodu
Polecenie
Wybierz, wśród czterech przedstawionych poniżej, prawidłową wartość prędkości samochodu.
Rozwiązanie
W momencie trafienia współrzędne paczki i samochodu muszą być równe:
\[\begin{matrix} \Large{\frac{gt^2}{2}}=h \\ gt^2=2h \\ t^2=\Large{\frac{2h}{g}}\\ t=\Large{\sqrt{\frac{2h}{g}}} \end{matrix}\]
Z pierwszego wzoru wyznaczamy \(v_2\): \(\displaystyle{v_2=v_1-\frac{\left | AB \right |}{\Large{\sqrt{\frac{2h}{g}}}}}\)
\[v_2=\large{\frac{v_1t-\left | AB\right |}{t}}=v_1-\frac{\left | AB\right |}{t}=v_1-\frac{\left | AB \right |}{\Large{\sqrt{\frac{2h}{g}}}}\]
Odpowiedź
Prędkość samochodu wynosiła \(\displaystyle{v_2=17\,\mathrm{\frac{m}{s}}}\).