Zadanie 2.3.2.3
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.3. Składanie ruchów - rzuty
  4. 2.3.2 Trening
  5. Zadanie 2.3.2.3

 Zadanie 2.3.2.3

Przyspieszenie normalne i styczne.
Ciało zostało rzucone poziomo z prędkością \(\displaystyle{v_x=15\, \mathrm{\frac{m}{s}}}\). Znajdź wartość przyspieszenia normalnego i stycznego do toru, po upływie \(1\) sekundy od początku ruchu ciała. Opór powietrza pomijamy.

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- prędkość początkowa: \(\displaystyle{v_x=15\,\mathrm{\frac{m}{s}}}\),
- czas, po upływie którego mamy wyznaczyć składowe przyspieszenia \(t=1\,\mathrm{s}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- wartość składowej przyspieszenia stycznej do toru \(a_s\),
- wartość składowej przyspieszenia normalnej do toru tzn. prostopadłej do wektora przyspieszenia stycznego \(a_n\).

Odpowiedź

Wartość przyspieszenia normalnego wynosi \(\displaystyle{a_n=8,32\,\mathrm{\frac{m}{s^2}}}\), zaś przyspieszenia stycznego wynosi \(\displaystyle{a_s=5,55\,\mathrm{\frac{m}{s^2}}}\).

Polecenie

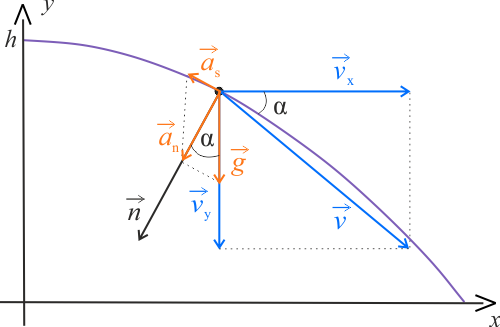
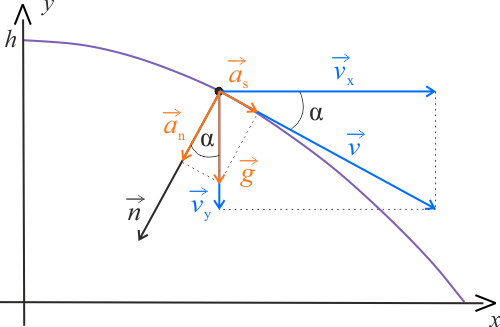
Narysuj rysunek przedstawiający rozkład przyspieszenia. Dodatkowo zaznacz wektor prędkości w tym punkcie. Wybierz jeden spośród dwóch rysunek, który najbardziej przypomina Twój.
 Jeżeli zaniedbamy siły związane z oporem powietrza, jedyną siłą działającą na ciało jest siła grawitacji. Związane z nią przyspieszenie jest stałe i skierowane zawsze prostopadle do ziemi. 

Wykres 1 z 2
Rzkład przyspieszenia i prędkości w rzucie poziomym

Odpowiedź nieprawidłowa.
Wektor prędkości nie jest styczny do toru ruchu.

Wykres 2 z 2
Rzkład przyspieszenia i prędkości w rzucie poziomym

Odpowiedź prawidłowa

Polecenie

Korzystając z rysunku wyznacz wartości odpowiednich funkcji trygonometrycznych. Wybierz jedną prawidłową odpowiedz z trzech podanych poniżej.

Wybór 1 z 3

\(\displaystyle{\cos\alpha=\frac{a_s}{g}}\)
\(\displaystyle{\cos\alpha=\frac{v_y}{v}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 3

\(\displaystyle{\cos\alpha=\frac{a_n}{g}}\)
\(\displaystyle{\cos\alpha=\frac{v_x}{v}}\)

Odpowiedź prawidłowa

Wybór 3 z 3

\(\displaystyle{\cos\alpha=\frac{a_n}{a_s}}\)
\(\displaystyle{\cos\alpha=\frac{v_x}{v_y}}\)

Odpowiedź nieprawidłowa

Polecenie

Wyznacz wartość przyspieszenia normalnego. Wybierz jedną, prawidłową wartość spośród dwóch podanych poniżej.

Wybór 1 z 2

\(\displaystyle{a_n=8,32\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\displaystyle{a_n=3,2\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Z rysunku można było odczytać, że \(\displaystyle{\cos\alpha=\frac{a_n}{g}}\) stąd mamy:

\(\displaystyle{a_n=g\,\cos\alpha}\)

Funkcję cosinus można również wyrazić jako \(\displaystyle{\cos\alpha=\frac{v_x}{v}}\). Podstawiając tą zależność do równania powyżej mamy:

\(\displaystyle{a_n=g\,\frac{v_x}{v}}\)

Wartość wektora prędkości wyznaczamy następująco:

\(v^2=v_x^2+v_y^2\)
\(v=\sqrt{v_x^2+v_y^2}\)

Rzut ukośny możemy rozpatrywać jako złożenie spadku swobodnego z ruchem poziomym ze stałą prędkością. Zatem po czasie \(t\) składowa pionowa prędkości ciała, która jest prędkością jaką osiągnie ciało w spadku swobodnym będzie równa \(v_y=gt\).

Podstawiając wyznaczone zależności do równania na \(a_n\) otrzymujemy:

\(\displaystyle{a_n=g\,\cos\alpha=g\frac{v_x}{v}=\frac{gv_x}{\sqrt{v_x^2+v_y^2}}=\frac{gv_x}{\sqrt{v_x^2+g^2\,t^2}}}\) 
\(\displaystyle{a_n=\frac{10\cdot 15}{\sqrt{15^2+10^2\cdot 1^2}}=\frac{150}{\sqrt{325}}=8,32}\)   \(\displaystyle{\mathrm{\left [ \frac{\frac{m}{s^2}\frac{m}{s}}{\sqrt{\left (\frac{m}{s}\right)^2+\left ( \frac{m^2}{s^2} \right )^2s^2}}=\frac{\frac{m^2}{s^3}}{\sqrt{\frac{m^2}{s^2}+\frac{m^2}{s^2}}}= \frac{m^2}{s^3}\frac{s}{m}=\frac{m}{s^2}\right ]}}\)



Polecenie

Wyznacz wartość przyspieszenie stycznego. Wybierz jedną, prawidłową wartość spośród dwóch podanych poniżej.

Wybór 1 z 2

\(\displaystyle{a_s=5,55\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\displaystyle{a_s=0,55\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Wartość wektora przyspieszenie stycznego wyznaczamy następująco: \(g^2=a_n^2+a_s^2\). Przyspieszenia styczne i normalne sa składowymi wektora \(\vec{g}\).

\(\displaystyle{a_s=\sqrt{g^2-a_n^2}=\sqrt{10^2-\frac{150^2}{325}}=5,55\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź

Wartość przyspieszenia normalnego wynosi \(\displaystyle{a_n=8,32\,\mathrm{\frac{m}{s^2}}}\), zaś przyspieszenia stycznego wynosi \(\displaystyle{a_s=5,55\,\mathrm{\frac{m}{s^2}}}\).