Zadanie 2.3.2.4
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.3. Składanie ruchów - rzuty
  4. 2.3.2 Trening
  5. Zadanie 2.3.2.4

 Zadanie 2.3.2.4

Rzut ukośny
Kamień wyrzucono z katapulty z prędkością początkową \(\displaystyle{v_0=20\, \mathrm{\frac{m}{s}}}\), pod kątem \(30^{\circ}\) do poziomu. Wyznacz położenie i prędkość kamienia po czasie \(t=1,2\, \mathrm{s}\).

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- prędkość początkowa kamienia: \(\displaystyle{v_0=20\,\mathrm{\frac{m}{s}}}\),
- czas, po upływie którego mamy wyznaczyć położenie i prędkość kamienia: \(t=1,2\,\mathrm{s}\),
- kąt pod jakim rzucono kamień \(\alpha=30^{\circ}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- wartość współrzędnej iksowej punktu, w którym znalazł się kamień po upływie \(1,2\,\mathrm{s}\): \(x\),
- wartość współrzędnej igrekowej punktu, w którym znalazł się kamień po upływie \(1,2\,\mathrm{s}\): \(y\),
- wartość prędkości kamienia po upływie \(1,2\,\mathrm{s}\): \(v\).

Odpowiedź

Po czasie \(t\) kamień znajdzie się w punkcie o współrzędnych \(x=12\sqrt{3}\,\mathrm{m}\) i \(y=4,8\,\mathrm{m}\), a jego prędkość wynosi \(\displaystyle{v=17,44\,\mathrm{\frac{m}{s}}}\).

Polecenie

Naszkicuj tor kamienia w kartezjańskim układzie współrzędnych i zastanów się, jak zmieniała się z czasem jego współrzędna \(x\) oraz \(y\). Wybierz jeden, wśród dwóch, prawidłowy wykres opisujący sytuację z treści zadania.

Wykres 1 z 2

Tor lotu kamienia

Odpowiedź nieprawidłowa
W kierunku osi \(x\) na kamień nie działają żadne siły, dlatego też składowa pozioma prędkości kamienia nie ulegała zmianie w czasie.

Wykres 2 z 2

Tor lotu kamienia

Odpowiedź prawidłowa

Polecenie

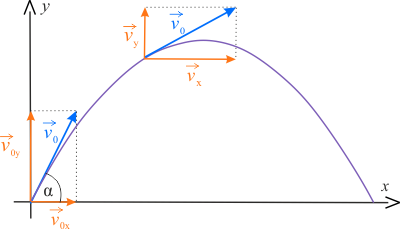
Korzystając z rysunku, wyznacz składowe wektora prędkości. Wybierz jeden, prawidłowy zestaw wzorów wśród dwóch, przedstawionych poniżej.

Wybór 1 z 2

\(v_x(t)=v_{0x}\,\sin\alpha\)
\(v_y(t)=v_{0y}+gt=v_0\,\sin\alpha+gt\)

Odpowiedź nieprawidłowa

Wybór 2 z 2

\(v_x(t)=v_{0x}=v_0\,\cos\alpha\)
\(v_y(t)=v_{0y}-gt=v_0\,\sin\alpha-gt\)

Odpowiedź prawidłowa

Rozwiązanie

W kierunku osi \(OX\) na kamień nie działają żadne siły, dlatego też składowa pozioma prędkości kamienia nie będzie ulegała zmianie w czasie i będzie miała wartość:

\(v_x(t)=v_{0x}=v_0\,\cos\alpha\)

Ruch w kierunku pionowym możemy traktować jako rzut pionowy do góry z prędkością początkową \(v_{0y}=v_0\,\sin\alpha\) i opóźnieniem \(g\). Prędkość w kierunku osi \(OY\) będzie zmieniała się z czasem jak:
\(v_y(t)=v_{0y}-gt=v_0\,\sin\alpha-gt\)

Polecenie

Korzystając z rysunku wyznacz składowe położenia. Wybierz jeden prawidłowy zestaw wzorów wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(x(t)=v_{0x}t=v_0\,\cos\alpha t\)
\(\displaystyle{y(t)=v_{0y}t-\frac{gt^2}{2}=v_0\,\sin\alpha t-\frac{gt^2}{2}}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(x(t)=v_{0x}t=v_0\,\sin\alpha t\)
\(\displaystyle{y(t)=\frac{gt^2}{2}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

W kierunku osi \(OX\) ruch odbywa się ze stała prędkością, dlatego też iksowa współrzędna położenia kamienia będzie zmieniała się z czasem jak:

\(x(t)=v_{0x}t=v_0\,\cos\alpha t\)
 
Ruch w kierunku pionowym możemy traktować jako rzut pionowy do góry, z prędkością początkową \(v_{0y}=v_0\,\sin\alpha\) i opóźnieniem \(g\). Igrekowa współrzędna położenia kamienia będzie zmieniała się z czasem, jak:
\(\displaystyle{y(t)=v_{0y}t-\frac{gt^2}{2}=v_0\,\sin\alpha t-\frac{gt^2}{2}}\)

Polecenie

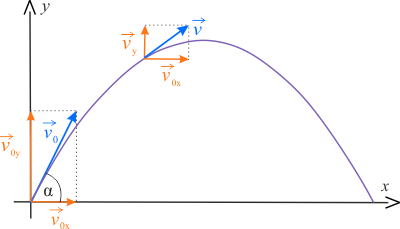
Oblicz wartość prędkości kamienia oraz współrzędne jego położenia po upływie \(1,2\,\mathrm{s}\). Wybierz jedną, prawidłową odpowiedź wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x=20\,\mathrm{m}\)
\(y=5\,\mathrm{m}\)
\(\displaystyle{v=15\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x=6\sqrt{2}\,\mathrm{m}\)
\(y=6\,\mathrm{m}\)
\(\displaystyle{v=6,5\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(x=12\sqrt{3}\,\mathrm{m}\)
\(y=4,8\,\mathrm{m}\)
\(\displaystyle{v=17,44\,\mathrm{\frac{m}{s}}}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(x=2\sqrt{3}\,\mathrm{m}\)
\(y=8\,\mathrm{m}\)
\(\displaystyle{v=1,44\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Współrzędne kamienia wynoszą:

\(x=v_0\cos\alpha t=20\cdot \cos 30^{\circ}\cdot 1,2\)  \(\displaystyle{=20 \cdot \frac{\sqrt{3}}{2}\cdot \frac{6}{5}}\)  \(=12\sqrt{3}\)
\(x=12\sqrt{3}\,\mathrm{m}\)

\(\displaystyle{y=v_0\sin\alpha t-\frac{1}{2}gt^2=20\cdot \frac{1}{2}\cdot \frac{6}{5}-\frac{1}{2}\cdot 10\cdot \frac{36}{25}=4,8}\)
\(y=4,8\,\mathrm{m}\)

Po czasie \(t\) prędkość kamienia będzie wynosić:
\(v=\sqrt{v_x^2+v_y^2}=\sqrt{v_0^2\cos^2 30^{\circ}+\left ( v_0\sin \alpha -gt \right )^2 }\)
\(\displaystyle{v=\sqrt{20^2\cdot \frac{3}{4}+\left ( 20\cdot \frac{1}{2} -10\cdot 1,2 \right )^2}=17,44}\)
\(\displaystyle{v=17,44\,\mathrm{\frac{m}{s}}}\)

Odpowiedź

Po czasie \(t\) kamień znajdzie się w punkcie o współrzędnych \(x=12\sqrt{3}\,\mathrm{m}\) i \(y=4,8\,\mathrm{m}\), a jego prędkość wynosi \(\displaystyle{v=17,44\,\mathrm{\frac{m}{s}}}\).