Zadanie 2.4.1.3
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.4. Ruch krzywoliniowy
  4. 2.4.1 Nauka
  5. Zadanie 2.4.1.3

 Zadanie 2.4.1.3

Ruch po okręgu
W muzeum pokazywano, jak działają maszyny proste. Na linie przewieszonej przez krążek, został zawieszony ciężarek. Na krążku zaznaczono punkt. Po odblokowaniu bloczka, ciężarek poruszał się ruchem jednostajnie przyspieszonym. Wyznacz, w zależności od czasu, przyspieszenie całkowite punktu zaznaczonego na obwodzie krążka.

 Wskazówka teoretyczna

 Teoria - ruch po okręgu
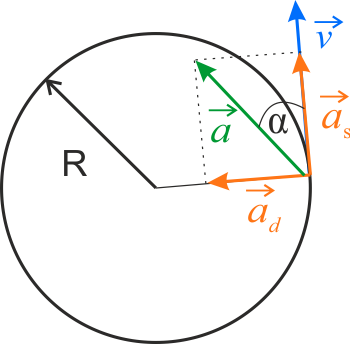
Przyspieszenie w ruchu po okręgu:

\(\vec{a}=\vec{a}_s+\vec{a}_d\)
 
\(\displaystyle{\varepsilon=\frac{\mathrm{d}\omega}{\mathrm{d}t}=\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}}\)
\(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}=\varepsilon R}\)
\(\displaystyle{a_d=\omega ^2 R=\frac{v^2}{R}}\)
\(\displaystyle{\operatorname{tg}{\alpha}={\frac{a_d}{a_s}}}\)
Przyspieszenie w ruchu po okręgu

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- równanie opisujące ruch ciężarka \(\displaystyle{s=\frac{1}{2}at^2}\).

Szukane:
- przyspieszenie całkowite punktu zaznaczonego na obwodzie krążka \(a\).

Analiza sytuacji

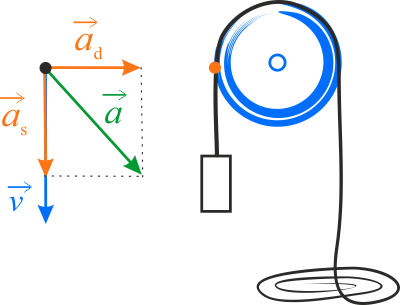
Po odblokowaniu bloczka ciężarek porusza się ruchem jednostajnie przyspieszonym. Prędkość poruszania się ciężarka jest taka sama, jak punktu zaznaczonego na krążku. Drogę, jaką przebywa punkt, czy klocek określa zależność:

\(\displaystyle{S=\frac{1}{2}\,at^2}\)
Znając zależność na drogę, można wyznaczyć prędkość \(\displaystyle{v=\frac{\mathrm{d}s }{\mathrm{d} t}}\), a stąd już prosta droga do poprawnego rozwiązania zadania. W tym momencie można skorzystać z zależności opisujących przyspieszenia w ruchu po okręgu:
\(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}}\)  oraz  \(\displaystyle{a_d=\frac{v^2}{R}}\)

Rysunek

Rozwiązanie

Prędkość poruszającego się ciężarka obliczamy z zależności:

\(\displaystyle{v=\frac{\mathrm{d}s }{\mathrm{d} t}=at}\)  \(\displaystyle{\frac{\mathrm{d}(\frac{1}{2}at^2) }{\mathrm{d} t}=\frac{1}{2}\cdot2\,at=at}\) 

Prędkość ciężarka jest taka sama, jak punktu zaznaczonego na krążku.
Aby wyznaczyć przyspieszenie całkowitego punktu należy skorzystać z zależności opisujących przyspieszenia w ruchu po okręgu:
\(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}}\)  oraz  \(\displaystyle{a_d=\frac{v^2}{R}}\)
 \(\displaystyle{a_s=\frac{\mathrm{d}at}{\mathrm{d} t}}\) oraz \(\displaystyle{a_d=\frac{(at)^2}{R}}\) 
\(\displaystyle{a_s=a}\)  oraz  \(\displaystyle{a_d=\frac{a^2 t^2}{R}}\)

Przyspieszenie całkowite wynosi:
\(a_c=\sqrt{a_s^2+a_d^2}\)
\(\displaystyle{a_c=\sqrt{a^2+\frac{a^4 t^4}{R^2}}=\frac{a}{R}\sqrt{R^2+a^2t^4}}\)

Odpowiedź

Przyspieszenie całkowite punktu, zaznaczonego na obwodzie krążka, wyznaczone w zależności od czasu, wynosi \(\displaystyle{a_c=\frac{a}{R}\sqrt{R^2+a^2t^4}}\).