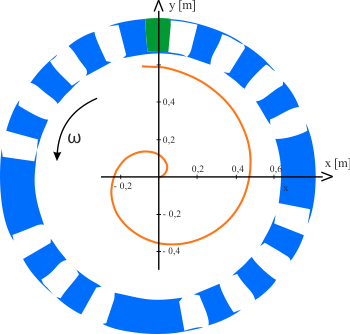
Zadanie 2.4.2.5
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.4. Ruch krzywoliniowy
  4. 2.4.2 Trening
  5. Zadanie 2.4.2.5

 Zadanie 2.4.2.5

 Kinematysław dla odważnych miał zadanie. Czy zerkniesz na nie?
Kinematysław postanowił zwiedzić koło fortuny o promieniu \(R\). Kiedy doszedł do środka koła, Fizaliusz zakręcił nim, nadając mu prędkość kątową \(\omega\). Kinematysław spokojnie skierował kroki, wzdłuż promienia, w stronę krawędzi koła. Wyznacz równanie ruchu kroczącego Kinematysława. Jak wyglądał tor ruchu według Kinematysława, a jak według Fizaliusza stojącego na zewnątrz? Wyznacz zależność od czasu wektora prędkości oraz jego składowych radialnej i transwersalnej, a także zależność od czasu wektora przyspieszenia oraz jego składowych: radialnej, transwersalnej, normalnej i stycznej.
Rysunek 1
Rysunek 2

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- promień koła \(R\),
- prędkość kątowa koła \(\omega\).

Szukane:
- Równanie ruchu Kinematysława,
- zależność od czasu wektora prędkości \(\vec{v}(t)\),
- składowe wektora prędkości \(v_r\), \(v_{\varphi}\),
- zależność od czasu wektora przyspieszenia \(\vec{a}(t)\),
- składowe wektora przyspieszenia \(a_r\), \(a_{\varphi}\), \(a_n\), \(a_s\).

Odpowiedź

Zależność od czasu wektora prędkości wynosi \(\displaystyle{v(t)=v_0\sqrt{1+\omega^2t^2}}\), a jego składowe można zapisać w postaci \(v_r=v_0\)  oraz \(v_{\varphi}=\omega v_0t\).

Zależność od czasu wektora przyspieszenia wynosi \(\displaystyle{a(t)=v_0\omega \sqrt{t^2\omega^2+4}}\).
Składowa radialna i transwersalna wektora przyspieszenia wynoszą: \(a_r=v_0\,t\,\omega^2\)  oraz \(a_{\varphi}=2\omega v_0\).

Składowa styczna i normalna wektora przyspieszenia wynoszą: \(\displaystyle{a_n=\frac{v_0\omega(\omega^2t^2+2)}{\sqrt{1+\omega^2t^2}}}\)  oraz \(\displaystyle{a_s=\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\).

Polecenie

Jak wyglądał tor ruchu według Kinematysława, a jak według Fizaliusza stojącego na zewnątrz? Wybierz prawidłową odpowiedź, z czterech przedstawionych poniżej.

Wybór 1 z 4

Kinematysław porusza się ruchem jednostajnym prostoliniowym, natomiast Fizaliusz obserwuje tor ruchu opisany elipsą.

Odpowiedź nieprawidłowa

Wybór 2 z 4

Kinematysław porusza się ruchem jednostajnym prostoliniowym, natomiast Fizaliusz obserwuje tor ruchu opisany cykloidą.

Odpowiedź nieprawidłowa

Wybór 3 z 4

Kinematysław porusza się ruchem jednostajnym prostoliniowym, natomiast Fizaliusz obserwuje tor ruchu opisany parabolą.

Odpowiedź nieprawidłowa

Wybór 4 z 4

Kinematysław porusza się ruchem jednostajnym prostoliniowym, natomiast Fizaliusz obserwuje tor ruchu opisany spiralą Archimedesa.

Odpowiedź prawidłowa

Rozwiązanie

W układzie odniesienia związanym z wirującym kołem, czyli z punktu widzenia Kinematysława, porusza on się wzdłuż promienia - ruch prostoliniowy jednostajny ze stałą prędkością. W układzie odniesienia związanym z nieruchomym Fizaliuszem, Kinematysław porusza się po spirali.

W celu wyznaczenia kształtu spirali posłużymy się układem biegunowym. W układzie tym równania ruchu wyrażone są przy pomocy współrzędnej radialnej \(r\) i kątowej \(\varphi\). Prędkość poruszania się obiektu wzdłuż promienia jest stała i wynosi \(v_0\), więc:

\(r=v_0t\)

W chwili początkowej \(t=0\) oraz wartość kąta wynosi zero. Koło obraca się ze stałą prędkością kątową \(\omega\) więc kąt zmienia się z czasem następująco:
\(\varphi=\omega t\)

Dwa powyższe równania przekształcamy tak, aby wyznaczyć czas:  \(\displaystyle{t=\frac{r}{v_0}}\)  oraz  \(\displaystyle{t=\frac{\varphi}{\omega}}\).
Po przyrównaniu obu równań otrzymujemy równanie ruchu zapisane we współrzędnych biegunowych.
\(\displaystyle{r=\frac{v_0}{\omega}\cdot \varphi}\)

Otrzymana zależność opisuje  Spirala Archimedesa - dwuwymiarowa krzywa o równaniu we współrzędnych biegunowych: \(r=s\cdot \varphi\), gdzie \(r\) - promień, \(s\) - parametr, \(\varphi\) - kąt.  .

Tor ruchu

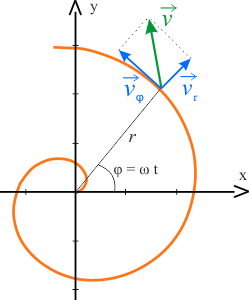
Polecenie

Wyznacz zależność od czasu wektora prędkości oraz jego składowych radialnej i transwersalnej. Wybierz jeden zestaw prawidłowych odpowiedzi, wśród dwóch zaproponowanych poniżej.

Zestaw 1 z 2

Składowe radialna i transwersalna wektora prędkości wynoszą odpowiednio:
\(\displaystyle{v_r=\varphi v_0}\)
\(\displaystyle{v_{\varphi}=\omega\, t}\)

Równanie opisujące prędkość obiektu w zależności od czasu, wyznaczamy następująco:
\(\displaystyle{v(t)=v_0^4\sqrt{1+\omega^2t^2}}\)

Odpowiedź nieprawidłowa

Zestaw 2 z 2

Składowe radialna i transwersalna wektora prędkości wynoszą odpowiednio:
\(\displaystyle{v_r=v_0}\)
\(\displaystyle{v_{\varphi}=\omega\, v_0t}\)

Równanie opisujące prędkość obiektu w zależności od czasu, wyznaczamy następująco:
\(\displaystyle{v(t)=v_0\sqrt{1+\omega^2t^2}}\)

Odpowiedź prawidłowa

Rozwiązanie - prędkość

Na rysunku obok narysowano składowe wektora prędkości, wyznaczone w układzie biegunowym.
Z definicji składowe te wynoszą:

\(\displaystyle{v_r=\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{\mathrm{d} (v_0t)}{\mathrm{d} t}=v_0}\)  oraz  \(\displaystyle{v_{\varphi}=\frac{\mathrm{d} \varphi}{\mathrm{d} t}r=\omega r=\omega\, v_0t}\)

Równanie opisujące prędkość obiektu w zależności od czasu, wyznaczamy następująco:

\(\displaystyle{v=\sqrt{v_r^2+v_{\varphi}^2}=v_0\sqrt{1+\omega^2t^2}}\)
\(\displaystyle{v(t)=v_0\sqrt{1+\omega^2t^2}}\)

Składowe wektora prędkości

Polecenie

Wyznacz zależność od czasu wektora przyspieszenia oraz jego składowych radialnej, transwersalnej, normalnej i stycznej. Wybierz jeden zestaw prawidłowych odpowiedzi, wśród dwóch zaproponowanych poniżej.

Zestaw 1 z 2

\(\displaystyle{a(t)=v_0\omega \sqrt{t^2\omega^2+4}}\)
\(a_r=v_0\,t\,\omega^2\)  oraz \(a_{\varphi}=2\omega v_0\)
\(\displaystyle{a_n=\frac{v_0\omega(\omega^2t^2+2)}{\sqrt{1+\omega^2t^2}}}\)  oraz \(\displaystyle{a_s=\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\)

Odpowiedź prawidłowa

Zestaw 2 z 2

\(\displaystyle{a(t)=\sqrt{t^2\omega^2+4}}\)
\(a_r=v_0\,t\)  oraz \(a_{\varphi}=2\omega^2 v_0\)
\(\displaystyle{a_n=\frac{v_0^2\omega^2(\omega t+2)}{\sqrt{1+\omega^2t^2}}}\)  oraz \(\displaystyle{a_s=\frac{v_0^2\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie - przyspieszenie we współrzędnych biegunowych

Całkowite przyspieszenie we współrzędnych biegunowych można rozłożyć na składowe radialną i transwersalną. Na podstawie definicji mamy:

\(\displaystyle{a_r=\frac{\mathrm{d^2}r}{\mathrm{d}t^2}-r\left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2=\frac{\mathrm{d^2}(v_0t)}{\mathrm{d}t^2}-r\,\omega^2}\)
\(\displaystyle{a_r=0-v_0\,t\,\omega^2=v_0\,t\,\omega^2}\)

\(\displaystyle{a_{\varphi}=r\frac{\mathrm{d^2}\varphi }{\mathrm{d} t^2}+2\frac{\mathrm{d}\varphi}{\mathrm{d}t}\frac{\mathrm{d} r}{\mathrm{d}t}=r\cdot 0+2\omega\frac{\mathrm{d}(v_0t)}{\mathrm{d} t}=2\omega v_0}\)

Wartość całkowitego przyspieszenia wyznaczamy następująco:
\(\displaystyle{a=\sqrt{a_r^2+a_{\varphi}^2}=\sqrt{(-v_0t\omega^2)^2+(2v_0\omega)^2}}\)
\(\displaystyle{a=\sqrt{v_0^2t^2\omega^4+4v_0^2\omega^2}}\)
\(\displaystyle{a(t)=v_0\omega \sqrt{t^2\omega^2+4}}\)

Składowe wektora przyspieszenia adialna i transwersalna

Rozwiązanie - przyspieszenie styczne i normalne

Otrzymaną wartość całkowitą przyspieszenia, można również rozłożyć na składową normalną i styczną. Wartość składowej stycznej przyspieszenia \(a_s\) w chwili czasu \(t\) dana jest wzorem:

\(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}=\frac{\mathrm{d} }{\mathrm{d} t}\left ( v_0\sqrt{1+\omega^2t^2} \right )=\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\)
 \[\displaystyle{a_s=\frac{\mathrm{d} }{\mathrm{d} t}\left (v_0 \left (1+\omega^2t^2\right )^{\frac{1}{2}}\right )=}\] \[\displaystyle{=v_0\frac{1}{2}\left (1+\omega^2t^2\right )^{-\frac{1}{2}}2\omega^2t=\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\] 

Przyspieszenie całkowite można zapisać w postaci;
\(a^2=a_s^2+a_n^2\)
\(a_n^2=a^2-a_s^2\)
\(\displaystyle{a_n^2=\left (v_0\omega\sqrt{t^2\omega^2+4}\right )^2-\left (\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}} \right )^2}\)
 \[a_n^2=v_0^2\omega^2(t^2\omega^2+4)-\frac{v_0^2\,\omega^4t^2}{1+\omega^2t^2}\] \[a_n^2=\frac{v_0^2\omega^2\left ( (t^2\omega^2+4)(1+\omega^2t^2)-\omega^2t^2 \right )}{1+\omega^2t^2}\] \[a_n^2=\frac{v_0^2\omega^2\left (t^2\omega^2+\omega^4t^4+4+4\omega^2t^2-\omega^2t^2 \right )}{1+\omega^2t^2}\]\[a_n^2=\frac{v_0^2\omega^2\left (\omega^4t^4+4+4\omega^2t^2\right )}{1+\omega^2t^2}\] 
\(\displaystyle{a_n^2=\frac{v_0^2\omega^2(\omega^2t^2+2)^2}{1+\omega^2t^2}}\)
\(\displaystyle{a_n=\sqrt{\frac{v_0^2\omega^2(\omega^2t^2+2)^2}{1+\omega^2t^2}}}\)
\(\displaystyle{a_n=\frac{v_0\omega(\omega^2t^2+2)}{\sqrt{1+\omega^2t^2}}}\)

Rysunek 2

Odpowiedź

Zależność od czasu wektora prędkości wynosi \(\displaystyle{v(t)=v_0\sqrt{1+\omega^2t^2}}\), a jego składowe można zapisać w postaci \(v_r=v_0\)  oraz \(v_{\varphi}=\omega v_0t\).

Zależność od czasu wektora przyspieszenia wynosi \(\displaystyle{a(t)=v_0\omega \sqrt{t^2\omega^2+4}}\).
Składowa radialna i transwersalna wektora przyspieszenia wynoszą: \(a_r=v_0\,t\,\omega^2\)  oraz \(a_{\varphi}=2\omega v_0\).

Składowa styczna i normalna wektora przyspieszenia wynoszą: \(\displaystyle{a_n=\frac{v_0\omega(\omega^2t^2+2)}{\sqrt{1+\omega^2t^2}}}\)  oraz \(\displaystyle{a_s=\frac{v_0\,\omega^2t}{\sqrt{1+\omega^2t^2}}}\).