Zadanie 3.2.2.3
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.2 Trening
  5. Zadanie 3.2.2.3

 Zadanie 3.2.2.3

Zmiana pędu
Piłka o masie \(0,5\,\mathrm{kg}\) uderza o doskonale gładką ścianę, ustawioną wzdłuż osi \(OY\), z prędkością \(\displaystyle{\vec{v}_1=(4\,\hat{i}+3\,\hat{j})\,\frac{m}{s}}\) i odbija się od niej doskonale sprężyście w czasie \(0,01\,\mathrm{s}\). Oblicz średnią siłę, z jaką piłka działa na ścianę.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa piłki \(m=0,5\,\mathrm{kg}\),
- prędkość piłki \(\displaystyle{\vec{v}_1=(4\,\hat{i}+3\,\hat{j})\,\frac{m}{s}}\),
- czas uderzenia \(\Delta t=0,01\,\mathrm{s}\).

Szukane:
- średnia siła z jaką piłka działa na ścianę \(\vec{F}_s\).

Odpowiedź

Średnia siła, z jaką piłka działa na ścianę wynosi \(\vec{F}_s=400\,\hat{i}\,[\mathrm{N}]\).

Polecenie

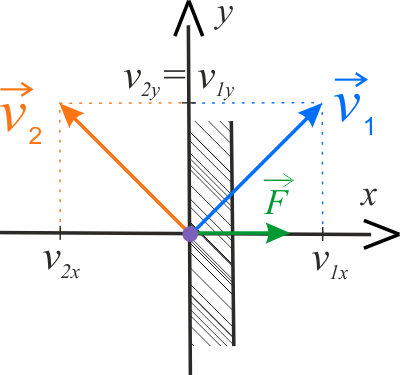
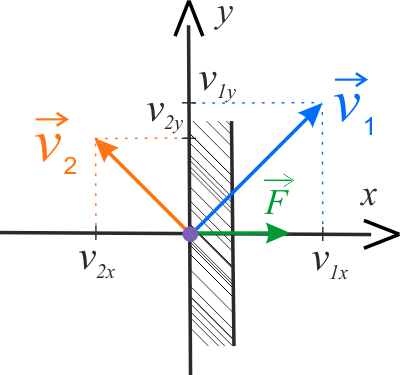
Sporządź rysunek ilustrujący treść zadania. Wybierz jedną prawidłową ilustrację, wśród dwóch przedstawionych poniżej.

Ilustracja 1 z 2

Rysunek 1a

Odpowiedź prawidłowa

Ilustracja 2 z 2

Rysunek 1b

Odpowiedź nieprawidłowa
Wektor prędkości \(\vec{v}_2\) ma za małą wartość. Przy zderzeniach sprężystych wartość prędkości nie ulega zmianie.

Polecenie

Poniżej przedstawiona jest część analizy fizycznej zadania. Wybierz jedną część, która, Twoim zdaniem, gwarantuje poprawne rozwiązanie zadania.

Zestaw 1 z 2

Podczas zderzenia ze ścianą piłka nie zmienia swojej prędkości. Zgodnie z II zasadą dynamiki zmiana pędu piłki wywołana jest siłą, z jaką działa na nią ściana. Siła, z jaką piłka działa na ścianę, będzie równa, co do wartości, tej sile, lecz będzie do niej przeciwnie skierowana (III zasada dynamiki). Aby obliczyć siłę, należy wyznaczyć siłę, z jaką działa na piłkę ściana.

Odpowiedź nieprawidłowa
Nie ulega zmianie wartość prędkość czyli szybkość. Wektor prędkości po zderzeniu różni się zwrotem i kieruniem.

Zestaw 2 z 2

Podczas zderzenia ze ścianą piłka zmienia swoją prędkość, a w związku z tym ulega zmianie również jej pęd. Zgodnie z II zasadą dynamiki zmiana pędu piłki wywołana jest siłą, z jaką działa na nią ściana. Siła, z jaką piłka działa na ścianę, będzie równa, co do wartości, tej sile, lecz będzie do niej przeciwnie skierowana (III zasada dynamiki). Aby obliczyć siłę należy wyznaczyć siłę, z jaką działa na piłkę ściana.

Odpowiedź prawidłowa

Polecenie

Wyznacz średnią siłę, z jaką piłka działa na ścianę. Wybierz jedną prawidłową odpowiedź, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\vec{F}_s=-400\,\hat{i}\,[\mathrm{N}]\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\vec{F}_s=200\,\hat{i}\,[\mathrm{N}]\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\vec{F}_s=400\,\hat{i}\,[\mathrm{N}]\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(\vec{F}_s=1600\,\hat{i}\,[\mathrm{N}]\)

Odpowiedź nieprawidłowa

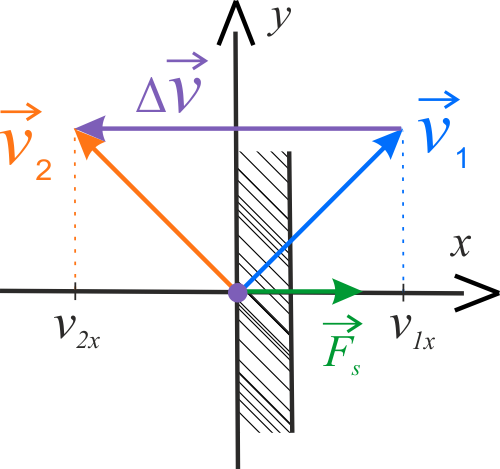
Rozwiązanie

Rysunek

Na rysunku przedstawiono prędkości piłki przed i po zderzeniu oraz ich różnicę. Ponieważ zderzenie piłki ze ścianą jest doskonale sprężyste, prędkość po zderzeniu musi mięć tę samą wartość, co prędkość przed zderzeniem, tzn. \(v_1=v_2\). Również składowa \(y\)-owa prędkości po odbiciu, musi mięć tę samą wartość, co przed odbiciem \((v_{2y}=v_{1y})\), gdyż w kierunku osi \(OY\) nie działa żadna siła (siła tarcia) – ściana jest doskonale gładka. Z analizy rysunku wynika, że, aby te dwa warunki były spełnione, to bezwzględne wartości \(x\)–owych składowych prędkości przed i po odbiciu muszą być sobie równe. Zatem:
\(v_{2x}=-v_{1x} \\ v_{2y}=v_{1y}\)
Stąd wynika, że prędkość po zderzeniu wynosi:
\(\displaystyle{\vec{v}_2=(-4\,\hat{i}+3\,\hat{j})\,\frac{m}{s}}\)
Z II zasady dynamiki mamy, że średnia siła działająca na piłkę w czasie zderzenia wynosi:
\(\displaystyle{\vec{F}=\frac{\Delta \vec{p}}{\Delta t}=m\,\frac{\Delta \vec{v}}{\Delta t}}\)
Obliczmy najpierw różnicę prędkości:
\(\Delta \vec{v}=\vec{v}_2-\vec{v}_1 \\ \Delta \vec{v}=-4\,\hat{i}+3\,\hat{j}-(4\,\hat{i}+3\,\hat{j})=-8\,\hat{i}\)
Siła \(\vec{F}_s\), którą piłka działa na ścianę, zgodnie z III zasadą dynamiki, wynosi:
\(\displaystyle{\vec{F}_s=-\vec{F}=-m\,\frac{\Delta \vec{v}}{\Delta t} \\ \vec{F}_s=-0,5\cdot \frac{-8\,\hat{i}}{0,01}=400\,\hat{i}\,[\mathrm{N}] }\)

Odpowiedź

Średnia siła, z jaką piłka działa na ścianę wynosi \(\vec{F}_s=400\,\hat{i}\,[\mathrm{N}]\).