Zadanie 3.2.2.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.2 Trening
  5. Zadanie 3.2.2.4

 Zadanie 3.2.2.4

Siła styczna i dośrodkowa
Statek kosmiczny o masie \(100\) ton poruszając się w przestrzeni kosmicznej, w czasie \(10\) minut pokonuje łuk równy połowie okręgu o promieniu \(300\,\mathrm{km}\). W tym czasie jego prędkość rośnie jednostajnie od \(\displaystyle{0\,\mathrm{\frac{km}{s}}}\) do \(\displaystyle{10\,\mathrm{\frac{km}{s}}}\). Jak podczas tego ruchu zmieniała się wartość jego siły stycznej i dośrodkowej?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa statku kosmicznego \(m=100\,\mathrm{ton}=10^5\,\mathrm{kg}\),
- promień okręgu po jakim porusza się statek kosmiczny \(R=300\,\mathrm{km}=3\cdot 10^5\,\mathrm{m}\),
- prędkość początkowa statku kosmicznego \(\displaystyle{v_0=0\,\mathrm{\frac{km}{s}}}\),
- prędkość końcowa statku kosmicznego \(\displaystyle{v_k=10\,\mathrm{\frac{km}{s}}}\),
- czas ruchu statku \(t_k=10\,\mathrm{min}=600\,\mathrm{s}\).

Szukane:
- wartość siły stycznej działającej statek kosmiczny \(F_s\),
- wartość siły dośrodkowej działającej statek kosmiczny \(F_d\).

Odpowiedź

Podczas lotu statku po łuku siła styczna osiąga wartość \(F_s=1,67\,\mathrm{MN}\). Siła dośrodkowa zmienia swą wartość w zależności od czasu następująco \(\displaystyle{F_d=92,6\cdot t^2\,\mathrm{\left [ \frac{N}{s^2}\cdot s^2 \right ]}}\).

Polecenie

Poniżej przedstawiona jest część analizy fizycznej zadania. Wybierz jedną część, która, Twoim zdaniem, gwarantuje poprawne rozwiązanie zadania.

Zestaw 1 z 2

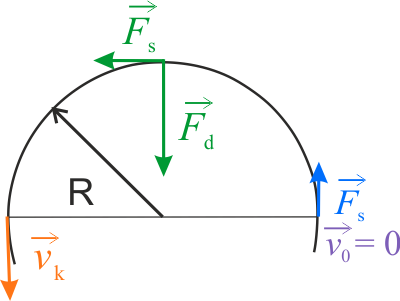
Statek kosmiczny porusza się po okręgu z rosnącą prędkością, więc musi na niego działać siła dośrodkowa \(F_d\), odpowiadająca za zmianę kierunku prędkości, jak również siła styczna \(F_s\), odpowiadająca za zmianę wartości prędkości. Z treści zadania wynika, poza tym, że prędkość statku kosmicznego rośnie jednostajnie, iż jego przyspieszenie styczne \(a_s\) zmienia się w czasie.

Odpowiedź nieprawidłowa
Przyspieszenie styczne \(a_s\) jest stałe w czasie przy jednostajnej zmianie prędkości.

Zestaw 2 z 2

Statek kosmiczny porusza się po okręgu z rosnącą prędkością, więc musi na niego działać siła dośrodkowa \(F_d\), odpowiadająca za zmianę kierunku prędkości, jak również siła styczna \(F_s\), odpowiadająca za zmianę wartości prędkości. Z treści zadania wynika, poza tym, że prędkość statku kosmicznego rośnie jednostajnie, iż jego przyspieszenie styczne \(a_s\) jest stałe.

Odpowiedź prawidłowa
Diagram wektorowy sił działających na statek kosmiczny
Diagram wektorowy sił działających na statek kosmiczny
Na rysunku przedstawiono diagram wektorowy sił działających na statek kosmiczny w chwili początkowej i w chwili, gdy statek pokonał \(\displaystyle{\frac{1}{4}}\) okręgu.

Polecenie

Wyznacz wartość siły stycznej. Wybierz jedna prawidłową wartość tej siły, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(F_s=1,67\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(F_s=20\,\mathrm{kN}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(F_s=1,67\,\mathrm{MN}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(F_s=2\,\mathrm{MN}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Siła styczna wyraża się wzorem:

\(\displaystyle{F_s=m\,a_s=m\frac{\mathrm{d} v}{\mathrm{d} t}=m\frac{v_k-v_0}{t_k}}\),

gdzie, ze względu na stałe przyspieszenie \(a_s\), zastąpiliśmy pochodną prędkości jej skończoną zmianą w czasie \(t\). Wnioskujemy, że wartość siły stycznej działającej na statek kosmiczny jest stała i wynosi:

\(\displaystyle{F_s=m\frac{v_k-v0}{t_k}=10^5\cdot \frac{10^4}{600}=1,67\,\mathrm{MN} }\)

Polecenie

Wyznacz zależność od czasu siły dośrodkowej. Wybierz jedno prawidłowe rozwiązanie, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{F_d=50,2\cdot t}\) 
\(\displaystyle{\left [\mathrm{\frac{N}{s}\cdot s}\right ]}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{F_d=50,2\cdot t^2}\) 
\(\displaystyle{\left [\mathrm{\frac{N}{s^2}\cdot s^2}\right ]}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{F_d=92,6\cdot t}\) 
\(\displaystyle{\left [\mathrm{\frac{N}{s}\cdot s}\right ]}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{F_d=92,6\cdot t^2}\) 
\(\displaystyle{\left [\mathrm{\frac{N}{s^2}\cdot s^2}\right ]}\)

Odpowiedź prawidłowa

Rozwiązanie

Wartość siły dośrodkowej dana jest wzorem

\(\displaystyle{F_d=m\,\frac{v^2}{R}}\).

Jak widać jej wartość rośnie z czasem, gdyż z czasem rośnie prędkość statku kosmicznego zgodnie z zależnością

\(v=a_s\,t\).

Zatem zależność wartości siły dośrodkowej działającej na statek kosmiczny od czasu wyraża się jako:

\(\displaystyle{F_d=m\,\frac{(a_s\,t)^2}{R}=\frac{m}{R}\frac{\left ( v_k-v_0 \right )^2}{t_k^2}\cdot t^2}\)
 \(\displaystyle{a_s=\frac{\mathrm{d} v}{\mathrm{d} t}=\frac{v_k-v_0}{t_k}}\) 
Po podstawieniu wartości liczbowych otrzymujemy:

\(\displaystyle{F_d=\frac{10^5}{3\cdot 10^5}\frac{\left ( 10^4 \right )^2}{600^2}\cdot t^2=92,6\cdot t^2}\) \(\displaystyle{\mathrm{\left [ \frac{kg}{m}\,\frac{\left ( \frac{m}{s} \right )^2}{s^2}\cdot s^2=\frac{kg}{m}\,\frac{m^2}{s^2}\,\frac{1}{s^2}\cdot s^2=kg\,\frac{m}{s^2}\,\frac{1}{s^2}\cdot s^2=\frac{N}{s^2}\cdot s^2 \right ]}}\)
\(\displaystyle{F_d=92,6\cdot t^2\,\left [\mathrm{\frac{N}{s^2}\cdot s^2}\right ]}\)
Jak widać wartość tej siły rośnie kwadratowo.

Komentarz

Ciekawe jest porównanie wartości obu sił po czasie \(t_k\). Wartość siły dośrodkowej po tym czasie wynosi

\(\displaystyle{F_d=92,6\,\mathrm{\frac{N}{s^2}}600^2\, \mathrm{s^2}=33\, 336\, 000\,\mathrm{N}=33\,\mathrm{MN} }\),

czyli jest około 20 razy większa od wartości siły stycznej.
\[\displaystyle{\frac{F_d}{F_s}=\frac{33336000}{1666667}\approx20}\]

Odpowiedź

Podczas lotu statku po łuku siła styczna osiąga wartość \(F_s=1,67\,\mathrm{MN}\). Siła dośrodkowa zmienia swą wartość w zależności od czasu następująco \(\displaystyle{F_d=92,6\cdot t^2\,\mathrm{\left [ \frac{N}{s^2}\cdot s^2 \right ]}}\).