Zadanie 3.2.2.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.2 Trening
  5. Zadanie 3.2.2.5

 Zadanie 3.2.2.5

Siła w ruchu po okręgu
Pewien przedmiot ślizga się bez tarcia, rozpoczynając z najwyższego punktu, po powierzchni półkoli o promieniu \(3\,\mathrm{m}\). Na jakiej wysokości ciało oderwie się od powierzchni kuli?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- promień kuli \(R=3\,\mathrm{m}\).

Szukane:
- wysokość, na jakiej ciało oderwie się od powierzchni kuli \(h\),

Odpowiedź

Ciało oderwie się od powierzchni kuli na wysokości \(\displaystyle{\frac{1}{3}R=1\,\mathrm{m}}\) (od podłoża to będzie \(2\,\mathrm{m}\) ).

Polecenie

Zastanów się, w którym punkcie ciało oderwie się od kuli. Wybierz jeden prawidłowy tok rozumowania, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

Ciało będzie poruszać się po powierzchni kuli do wysokości \(\frac{1}{2}\) promienia, ponieważ na tej wysokości nabiera odpowiedniej prędkości do oderwania się od powierzchni.

Odpowiedź nieprawidłowa

Wybór 2 z 2

Ciało będzie poruszać się po powierzchni kuli dopóki składowa jego ciężaru, wytyczona w kierunku promienia, nie zostanie zrównoważona przez siłę odśrodkową.

Odpowiedź prawidłowa

Polecenie

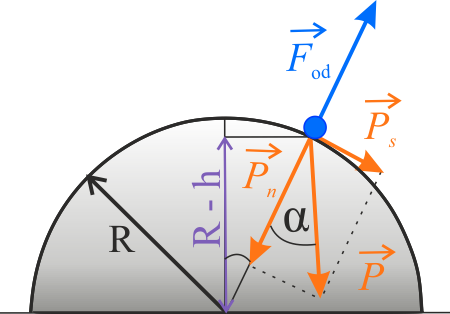
Na podstawie poniższego rysunku zastanów się, z jakich praw należy skorzystać, aby rozwiązać zadanie.
Wybierz, wśród dwóch, jeden układ równań umożliwiający otrzymanie prawidłowej odpowiedzi.

Rysunek

Wybór 1 z 2

\(\left\{\begin{matrix} mg=\large{\frac{mv^2}{R}}\\ mgh=\frac{1}{2}mv^2 \end{matrix}\right.\)

Odpowiedź nieprawidłowa
Składowa ciężaru ciała, wytyczona w kierunku promienia, ma zostać zrównoważona przez siłę odśrodkową, a nie ciężar ciała.

Wybór 2 z 2

\(\left\{\begin{matrix} mg\,\cos \alpha=\large{\frac{mv^2}{R}}\\ mgh=\frac{1}{2}mv^2 \end{matrix}\right.\)

Odpowiedź prawidłowa

Rozwiązanie

Ciało będzie poruszać się po powierzchni kuli dopóki składowa jego ciężaru, wytyczona w kierunku promienia \(\vec{P}_n\), nie zostanie zrównoważona przez siłę odśrodkową. Składową tą wyznaczamy z zależności:

\(\displaystyle{\cos\alpha=\frac{P_n}{P}}\)
\(P_n=mg\,\cos\alpha\)

Następnym krokiem jest przyrównanie tej siły do siły dośrodkowej:
\(\displaystyle{mg\,\cos\alpha=\frac{mv^2}{R}}\)
\(\displaystyle{\cos\alpha=\frac{v^2}{Rg}}\)

Cosinus kąta \(\alpha\) można również zapisać jako:
\(\displaystyle{\cos\alpha=\frac{R-h}{R}}\)
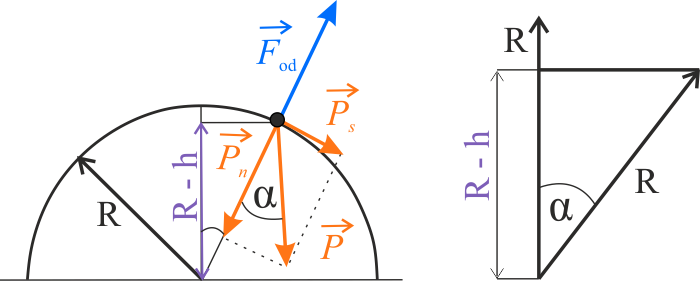
Rysunek


Po porównaniu dwóch funkcji cosinus mamy:

\(\displaystyle{\frac{R-h}{R}=\frac{v^2}{Rg} }\)
\(g(R-h)=v^2\)
Jest to pierwsze równanie układu równań.
Drugie równanie wynika z  Zasada zachowania energii w polu sił zachowawczych: \(\Delta E_p+\Delta E_k=0\). Innymi słowy, każda zmiana energii kinetycznej \(E_k\) jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej \(E_p\) układu, tak że ich suma pozostaje przez cały czas stała: \(E_k+E_p=const\).  :
\(E_p=E_k\)
\(\displaystyle{mgh=\frac{1}{2}mv^2}\)

W ten sposób z postaci:
\(\left\{\begin{matrix} mg\,\cos \alpha=\large{\frac{mv^2}{R}}\\ mgh=\frac{1}{2}mv^2 \end{matrix}\right.\)
uzyskujemy układ równań:
\[\left\{\begin{matrix} g(R-h)=v^2\\ gh=\frac{1}{2}v^2 \end{matrix}\right.\]

Polecenie

Wyznacz wysokość, na jakiej ciało oderwie się od powierzchni kuli. Wybierz jeden prawidłowy wynik, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(h=0,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(h=1\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(h=1,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(h=2\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Udzielenie prawidłowej odpowiedzi na pytanie zadania, wymaga rozwiązanie poniższego układu równań.

\(\left\{\begin{matrix} g(R-h)=v^2\\ gh=\frac{1}{2}v^2 \end{matrix}\right.\)

\(\eqalign{g(R-h) &=2gh \\ R-h &=2h \\ h &=\frac{1}{3}R }\)
Po podstawieniu wartości liczbowych otrzymujemy:
\(\displaystyle{h=\frac{1}{3}R=\frac{1}{3}\cdot 3=1\,\mathrm{m}}\)

Informacja

Poniżej, w postaci animacji, przedstawiono obliczenia odpowiadające na pytania:
1. Jaką drogę przebędzie przedmiot po powierzchni kuli od szczytu do momentu oderwania?
2. Jaką prędkość osiągnie przedmiot w momencie oderwania od powierzchni kuli?

W celu uzyskania odpowiedzi kliknij w niebieskie koła, umieszczone pod rysunkiem.

Odpowiedź

Ciało oderwie się od powierzchni kuli na wysokości \(\displaystyle{\frac{1}{3}R=1\,\mathrm{m}}\) (od podłoża to będzie \(2\,\mathrm{m}\) ).