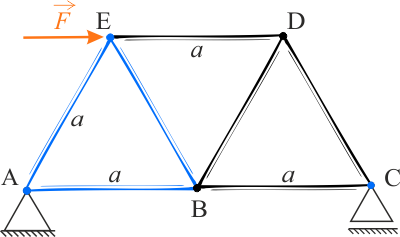
Zadanie 3.5.2.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.2 Trening
  5. Zadanie 3.5.2.4

 Zadanie 3.5.2.4

Kratownica
Z nieważkich prętów o takiej samej długości \(a\) zbudowano kratownice pokazaną na rysunku. Kratownica jest połączona przegubowo w punkcie \(A\), natomiast w punkcie \(C\) jest podparta, a do punktu \(E\) przyłożono poziomą siłę \(F=1\,\mathrm{kN}\). Wyznacz siły reakcji podłoża oraz siły działające w prętach oznaczonych kolorem niebieskim: \(F_{AB}\), \(F_{AE}\) oraz \(F_{BE}\).

 Rysunek

Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- wartość przyłożonej siły \(F=1\,\mathrm{kN}\).

Szukane:
- wartość siły reakcji podłoża w punkcie \(A\): \(R_{AX}\) i \(R_{AY}\),
- wartość siły reakcji podłoża w punkcie \(C\): \(R_{C}\),
- siły działające w prętach: \(F_{AB}\), \(F_{AE}\) oraz \(F_{BE}\).

Odpowiedź

Siły reakcji podłoża wynoszą: \(R_{AX}=1\,\mathrm{kN}\), \(R_{AY}=-433\,\mathrm{N}\) oraz \(R_{C}=433\,\mathrm{N}\), natomiast siły działające w prętach maja wartość: \(F_{AB}=750\,\mathrm{N}\), \(F_{AE}=500\,\mathrm{N}\) oraz \(F_{BE}=-500\,\mathrm{N}\).

Polecenie

Korzystając z warunku równowagi napisz równania opisujące działanie sił oraz momentów sił. Wybierz jeden prawidłowy zestaw równań, spośród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(\sum F_X=F-R_{AX}=0\)
\(\sum F_Y=R_{AY}+R_C=0\)
\(\sum M=F\cdot a\cdot \sin 60^{\circ}-R_C\cdot 2a=0\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\sum F_X=F-R_{AX}=0\)
\(\sum F_Y=-R_{AY}+R_C=0\)
\(\sum M=F\cdot a-R_C\cdot 2a=0\)

Odpowiedź nieprawidłowa

Rozwiązanie

Krok pierwszy rozwiązania polega na skorzystaniu z warunku równowagi i rozpisaniu działających sił oraz momentów sił. W tym celu wykonano rysunek.

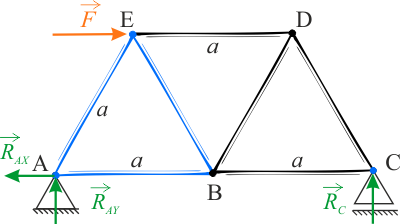
Rysunek


Poziomo, jak i pionowo, działają dwie siły:
\(\sum F_X=F-R_{AX}=0\)
\(\sum F_Y=R_{AY}+R_C=0\)

Momenty sił względem punktu \(A\) wynoszą:

\(\sum M=F\cdot a\cdot \sin 60^{\circ}-R_C\cdot 2a=0\)

Odległość prostej, na której leży wektor \(R_C\) od punktu \(A\) wynosi \(2a\), natomiast odległość prostej, na której leży wektor \(F\) od punktu \(A\) jest równa wysokości trójkąta równobocznego. Odległość tą można też zapisać jako \(\displaystyle{h=\frac{a\sqrt{3} }{2} }\).

Polecenie

Oblicz wartości sił \(R_{AX}\), \(R_{AY}\) oraz \(R_C\). Wybierz prawidłową odpowiedź, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(R_{AX}=433\,\mathrm{N}\)
\(R_{AY}=500\,\mathrm{N} \)
\(R_{C}=-500\,\mathrm{N} \)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(R_{AX}=500\,\mathrm{N}\)
\(R_{AY}=1\,\mathrm{kN} \)
\(R_{C}=433\,\mathrm{N} \)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(R_{AX}=1\,\mathrm{kN}\)
\(R_{AY}=-433\,\mathrm{N} \)
\(R_{C}=433\,\mathrm{N} \)

Odpowiedź prawidłowa

Wybór 4 z 4

\(R_{AX}=1\,\mathrm{kN}\)
\(R_{AY}=-500\,\mathrm{N} \)
\(R_{C}=500\,\mathrm{N} \)

Odpowiedź nieprawidłowa

Rozwiązanie

Z poprzednich rozważań warunku równowagi otrzymaliśmy równania:

\(\sum F_X=F-R_{AX}=0\)
\(\sum F_Y=R_{AY}+R_C=0\)
\(\sum M=F\cdot a\cdot \sin 60^{\circ}-R_C\cdot 2a=0\)

Z pierwszego równania mamy:
\(R_{AX}=F=1\,\mathrm{kN}\)
Z drugiego równania otrzymujemy:
\(R_{AY}=-R_C\)

Otrzymane wielkości podstawiamy do równania trzeciego i otrzymujemy:

\(\displaystyle{F\cdot \frac{\sqrt{3}}{2}=R_{C}\cdot 2 }\)
\(\displaystyle{R_{C}=F\cdot \frac{\sqrt{3}}{4}}\)
\(\displaystyle{R_{C}=1000\cdot \frac{\sqrt{3}}{4}=433\,\mathrm{N} }\)

\(R_{AY}=-433\,\mathrm{N} \)

Polecenie

Następnym krokiem rozwiązania zadania jest rozważenie sił działających w każdym z węzłów z osobna oraz napisanie równań dla każdego węzła z rozróżnieniem składowych iksowych i igrekowych. Napisz równania dla węzłów w punktach \(A\) i \(E\). Wybierz jeden prawidłowy zestaw równań, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

Dla węzła w punkcie \(A\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &= -R_{AX}+F_{AB}+F_{AE}\cdot \cos 60^{\circ}=0 \\ \sum F_y &=R_{AY}+F_{AE}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(E\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=F+F_{ED}-F_{AE}\cdot \cos 60^{\circ}+F_{BE}\cdot \cos 60^{\circ} =0 \\ \sum F_y &=-F_{AE}\cdot \sin 30^{\circ}-F_{BE}\cdot \sin 30^{\circ} =0 \end{cases} \end{eqnarray} \)

Odpowiedź prawidłowa

Wybór 2 z 2

Dla węzła w punkcie \(A\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &= -R_{AX}+F_{AB}+F_{AE}\cdot \cos 30^{\circ}=0 \\ \sum F_y &=R_{AY}+F_{AE}\cdot \sin 30^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(E\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=F+F_{ED}-F_{AE}\cdot \cos 30^{\circ}+F_{BE}\cdot \cos 30^{\circ} =0 \\ \sum F_y &=-F_{AE}\cdot \sin 15^{\circ}-F_{BE}\cdot \sin 15^{\circ} =0 \end{cases} \end{eqnarray} \)

Odpowiedź nieprawidłowa

Rozwiązanie

Napisanie prawidłowych równań, znacznie ułatwią rysunki działających sił w poszczególnych węzłach.

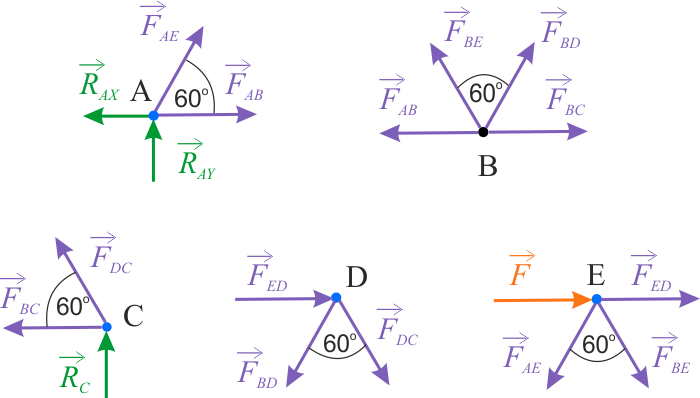
Rysunek


Dla węzła w punkcie \(A\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &= -R_{AX}+F_{AB}+F_{AE}\cdot \cos 60^{\circ}=0 \\ \sum F_y &=R_{AY}+F_{AE}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(E\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=F+F_{ED}-F_{AE}\cdot \cos 60^{\circ}+F_{BE}\cdot \cos 60^{\circ} =0 \\ \sum F_y &=-F_{AE}\cdot \sin 30^{\circ}-F_{BE}\cdot \sin 30^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(B\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=-F_{AB}+F_{BC}-F_{BE}\cdot \cos 60^{\circ}+F_{BD}\cdot \cos 60^{\circ} =0 \\ \sum F_y &=F_{BE}\cdot \sin 60^{\circ}+F_{BD}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(C\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=-F_{BC}-F_{DC}\cdot \cos 60^{\circ} =0 \\ \sum F_y &=R_{C}+F_{DC}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Dla węzła w punkcie \(D\) mamy:
\(\begin{eqnarray} \begin{cases} \sum F_x &=F_{ED}-F_{BD}\cdot \cos 60^{\circ}+ F_{DC}\cdot \cos 60^{\circ}=0 \\ \sum F_y &=-F_{BD}\cdot \sin 60^{\circ}-F_{BC}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Polecenie

Oblicz wartości sił działających w prętach \(F_{AB}\), \(F_{AE}\) oraz \(F_{BE}\). Wybierz prawidłową odpowiedź, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(F_{AB}=750\,\mathrm{N}\)
\(F_{AE}=-700\,\mathrm{N}\)
\(F_{BE}=-500\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(F_{AB}=1000\,\mathrm{N}\)
\(F_{AE}=750\,\mathrm{N}\)
\(F_{BE}=-500\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(F_{AB}=100\,\mathrm{N}\)
\(F_{AE}=-500\,\mathrm{N}\)
\(F_{BE}=-500\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(F_{AB}=750\,\mathrm{N}\)
\(F_{AE}=500\,\mathrm{N}\)
\(F_{BE}=-500\,\mathrm{N}\)

Odpowiedź prawidłowa

Rozwiązanie

Obliczanie wartości sił należy wykonywać w takiej kolejności, aby w węźle maksymalnie dwie siły były nieznane. Zakłada się, że pręty są rozciągane. Wynik ujemny oznacza, że pręt jest ściskany. W tej sytuacji można rozpocząć od węzła \(A\).

Dla węzła w punkcie \(A\) otrzymaliśmy:

\(\begin{eqnarray} \begin{cases} \sum F_x &= -R_{AX}+F_{AB}+F_{AE}\cdot \cos 60^{\circ}=0 \\ \sum F_y &=R_{AY}+F_{AE}\cdot \sin 60^{\circ} =0 \end{cases} \end{eqnarray} \)

Z drugiego równania mamy

\(\displaystyle{F_{AE}=-\frac{R_{AY}}{\sin 60^{\circ}} }\)
\(\displaystyle{F_{AE}=-F\frac{\sqrt{3}}{4}:\frac{\sqrt{3}}{2} }\)
\(\displaystyle{F_{AE}=-1000\frac{\sqrt{3}}{4}\cdot \frac{2}{\sqrt{3}}=500\,\mathrm{N} }\)

Z pierwszego równania mamy
\(F_{AB}=R_{AX}-F_{AE}\cdot \cos 60^{\circ}\)
\(F_{AB}=1000-500\cdot 0,5=750\,\mathrm{N} \)

Dla węzła w punkcie \(E\) otrzymaliśmy

\(\begin{eqnarray} \begin{cases} \sum F_x &=F+F_{ED}-F_{AE}\cdot \cos 60^{\circ}+F_{BE}\cdot \cos 60^{\circ} =0 \\ \sum F_y &=-F_{AE}\cdot \sin 30^{\circ}-F_{BE}\cdot \sin 30^{\circ} =0 \end{cases} \end{eqnarray} \)

Z powyższego układu równań wystarczy skorzystać z równania drugiego i wyznaczyć wartość \(F_{BE}\)

\(F_{BE}\cdot \sin 30^{\circ}=-F_{AE}\cdot \sin 30^{\circ}\)
\(F_{BE} =-F_{AE}=-500\,\mathrm{N} \)

Odpowiedź

Siły reakcji podłoża wynoszą: \(R_{AX}=1\,\mathrm{kN}\), \(R_{AY}=-433\,\mathrm{N}\) oraz \(R_{C}=433\,\mathrm{N}\), natomiast siły działające w prętach maja wartość: \(F_{AB}=750\,\mathrm{N}\), \(F_{AE}=500\,\mathrm{N}\) oraz \(F_{BE}=-500\,\mathrm{N}\).