Zadanie 3.5.2.5
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa odważnika \(M=10\,\mathrm{kg}\),
- masa przedramienia razem z dłonią \(m=3\,\mathrm{kg}\),
- kąt zgięcia ręki w pozycji pierwszej \(\alpha_1= 90^{\circ}\),
- kąt zgięcia ręki w pozycji drugiej \(\alpha_2= 150^{\circ}\),
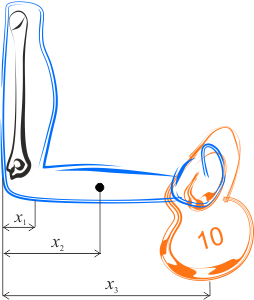
- oddalenie punktu przyłożenia siły mięśnia od stawu \(x_1=0,05\,\mathrm{m}\),
- oddalenie środka ciężkości przedramienia z dłonią \(x_2=0,15\,\mathrm{m}\),
- oddalenie środka ciężkości przedramienia z dłonią \(x_3=0,35\,\mathrm{m}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- wartość siły, z jaką działa mięsień ramienia w przypadku, gdy ręka jest zgięta pod kątem \(\alpha_1\): \(F_{m1}\),
- wartość siły, z jaką działa mięsień ramienia w przypadku, gdy ręka jest zgięta pod kątem \(\alpha_2\): \(F_{m2}\).
Odpowiedź
Mięsień ramienia działa z siłą \(F_m=790\,\mathrm{N}\), niezależnie od kąta zgięcia ręki.
Polecenie
Oblicz wartość siły, z jaką działa mięsień ramienia w przypadku, gdy ręka jest zgięta pod kątem \(\alpha_1\). Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.
\(F_{m1}=790\,\mathrm{N}\)
\(F_{m1}=800\,\mathrm{N}\)
Rozwiązanie
Rozrysujmy siły, jakie działają podczas trzymania ciężarka.
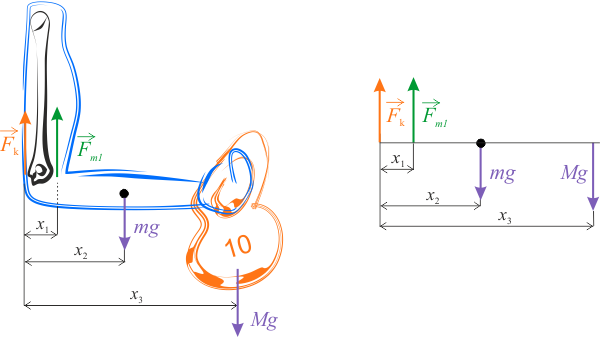
Siła \(\vec{F_k}\) jest siłą wywieraną przez kość ramienia. Wartości tej siły nie znamy, więc najwygodniej będzie przyjąć, że siła ta leży na osi obrotu. W zadaniu tym najprościej jest zastosować warunek zerowania się momentu siły. Na powyższym rysunku, po prawej stronie, pokazano uproszczony schemat działania sił. Na jego podstawie mamy:
Polecenie
Oblicz wartość siły, z jaką działa mięsień ramienia w przypadku, gdy ręka jest zgięta pod kątem \(\alpha_2\). Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.
Rozwiązanie
W tym przypadku ręka trzymana jest pod innym kątem. Punkty przyłożenia siły pozostają te same. Na rysunku poniżej pokazano uproszczony schemat działania sił.
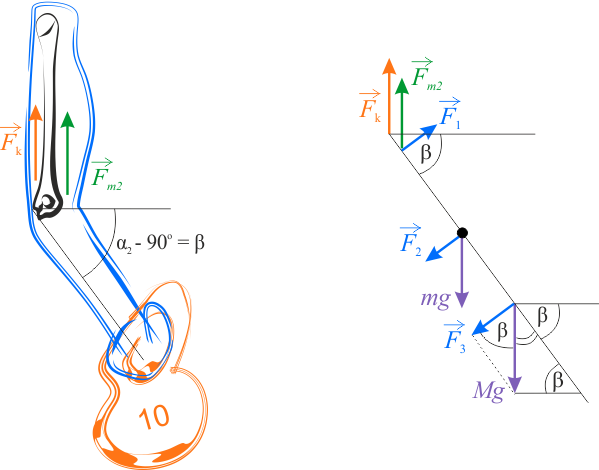
Część ręki, na którą działają siły, jest obrócona, w stosunku do poprzedniej sytuacji, o kąt \(\beta=150^{\circ}-90^{\circ}=60^{\circ}\). Na uproszczonym schemacie zaznaczono składowe działających sił \(\vec{F_1}\), \(\vec{F_2}\) oraz \(\vec{F_3}\) skierowane pionowo w stosunku do przedramienia. Podobnie, jak poprzednio, przyjęliśmy, że siła \(\vec{F_k}\) wywierana przez kość ramienia leży na osi obrotu.
Z warunku równowagi momentów sił mamy:
Korzystając z własności funkcji trygonometrycznych mamy:
Odpowiedź
Mięsień ramienia działa z siłą \(F_m=790\,\mathrm{N}\), niezależnie od kąta zgięcia ręki.