Zadanie 4.1.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa pociągu \(m=100\,\mathrm{t}=10^5\,\mathrm{kg}\),
- kąt nachylenia toru do poziomu \(\alpha=30^{\circ}\),
- przyspieszenie pociągu \(\displaystyle{a=1,5\,\mathrm{\frac{m}{s^2}}}\),
- droga przebyta przez pociąg \(S=150\,\mathrm{m}\),
- wartość efektywnego współczynnika tarcia kinetycznego \(\mu=0,05\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- praca, jaką wykonał silnik pociągu \(W\).
Odpowiedź
Silnik pociągu wykonał pracę \(W=104\,\mathrm{MJ}\).
Polecenie
Poniżej znajdują się dwa opisy sił działających na pociąg. Wybierz jeden prawidłowy.
Na pociąg elektryczny działają siły: siła napędowa silnika w kierunku ruchu pociągu \(F\), siła ciężkości \(P\) prostopadle do siły \(F\), siła reakcji podłoża \(R\) prostopadle do podłoża w górę oraz siła tarcia kinetycznego \(T\) przeciwnie do kierunku ruchu.
Polecenie
Wyznacz równanie opisujące siłę działającą na pociąg. Wybierz jedno prawidłowe, wśród dwóch przedstawionych poniżej.
\(F=m(a+g\sin\alpha+\mu g\cos\alpha)\)
\(F=m(g\sin\alpha+\mu g\cos\alpha)\)
Rozwiązanie
Aby wyznaczyć pracę siły napędowej, musimy najpierw wyznaczyć samą siłę, a następnie możemy z definicji pracy obliczyć pracę tej siły.
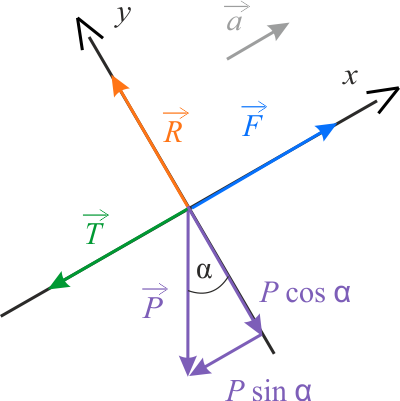
Na rysunku przedstawiono diagram sił działających na pociąg w dwuwymiarowym układzie współrzędnych \(x\;y\), gdzie oś \(x\) jest skierowana równolegle do toru w gorę, a oś \(y\) jest do niej prostopadła i skierowana w górę. \(F\) oznacza siłę napędową pociągu. Na podstawie diagramu możemy zapisać II zasadę dynamiki dla sił działających w kierunku \(x\) oraz warunek równowagi sił działających kierunku \(y\):
gdzie siła tarcia kinetycznego \(T=\mu N\), a \(N\) jest siłą nacisku pociągu na tor. Zgodnie z III zasadą dynamiki siła nacisku jest, co do wartości równa, sile reakcji podłoża \(N=R\). Zgodnie z warunkiem równowagi sił dla kierunku \(y\) mamy \(R=mg\cos\alpha\). Z powyższego układu równań otrzymujemy:
Polecenie
Wyznacz wartość pracy, jaką wykona siła \(F\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.
Rozwiązanie
Ponieważ siła \(F\) działa wzdłuż toru, to jej praca, na drodze \(S\), wyraża się wzorem:
W treści zadania występuje sformułowanie „efektywny współczynnik tarcia”. Siła tarcia, która hamuje ruch pociągu, występuje głównie na osiach kół wagonów częściowo na styku kół i szyn (można również uwzględnić siłę oporu powietrza). Jeżeli wartość sumarycznej siły tarcia zapiszemy jako \(T=\mu N\) to \(\mu\) jest właśnie efektywnym współczynnikiem tarcia.
Odpowiedź
Silnik pociągu wykonał pracę \(W=104\,\mathrm{MJ}\).
