Zadanie 4.2.2.2
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.2. Zasada zachowania energi
  4. 4.2.2 Trening
  5. Zadanie 4.2.2.2

 Zadanie 4.2.2.2

Zasięg ześlizgujących się sanek
Sanki ześlizgują się z pagórka, którego zbocze ma długość \(12\,\mathrm{m}\) i jest nachylone pod kątem \(30^{\circ}\) do poziomu. Po zjechaniu z pagórka, sanki poruszają się dalej po poziomej drodze. Jaką odległość przebędą sanki na odcinku poziomym. Na całej drodze (wzgórze oraz płaski odcinek) współczynnik tarcia sanek o drogę wynosi \(0,2\)?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- kąt nachylenia zbocza \(\alpha=30^{\circ}\),
- długość zbocza pagórka \(l=12\,\mathrm{m}\),
- współczynnik tarcia (kinetycznego) na całej drodze \(\mu=0,2\).

Szukane:
- odległość, jaką przebędą sanki na odcinku poziomym po zjechaniu ze zbocza \(x\).

Odpowiedź

Na odcinku poziomym sanki przebędą drogę \(19,6\,\mathrm{m}\).

Polecenie

Poniżej przedstawione są dwa twierdzenia. Wybierz jedno prawidłowe.

Stwierdzenie 1 z 2

Podczas zjeżdżania sanek z pagórka oraz ich ruchu po płaskiej nawierzchni, aż do zatrzymania się, następuje zamiana energii potencjalnej sanek tylko na energię kinetyczną.

Odpowiedź nieprawidłowa

Stwierdzenie 2 z 2

Podczas zjeżdżania sanek z pagórka oraz ich ruchu po płaskiej nawierzchni, aż do zatrzymania się, następuje zamiana energii mechanicznej sanek na energię wewnętrzną (cieplną) płóz sanek i podłoża.

Odpowiedź prawidłowa
Podczas zjeżdżania sanek z pagórka oraz ich ruchu po płaskiej nawierzchni, aż do zatrzymania się, następuje zamiana energii mechanicznej sanek na energię wewnętrzną (cieplną) płóz sanek i podłoża. Wartość bezwzględna pracy siły tarcia jest równa ubytkowi całej energii mechanicznej sanek, czyli ich początkowej energii potencjalnej. W celu rozwiązania zadania należy skorzystać ze związku pomiędzy pracą siły niezachowawczej (tutaj pracy siły tarcia), a zmianą energii całkowitej ciała.

Polecenie

Oblicz, jaką odległość przebędą sanki na odcinku poziomym. Wybierz prawidłowy wynik, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x=9,6\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x=12,2\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(x=19,6\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(x=26,4\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Skorzystamy ze związku pomiędzy pracą siły tarcia, a zmianą energii całkowitej sanek:

\(W_T=E_{konc}-E_{pocz}\),

gdzie \(E_{pocz}=mgh\) to energia początkowa sanek, a \(E_{konc}=0\) ich energia końcowa (sanki zatrzymały się). 

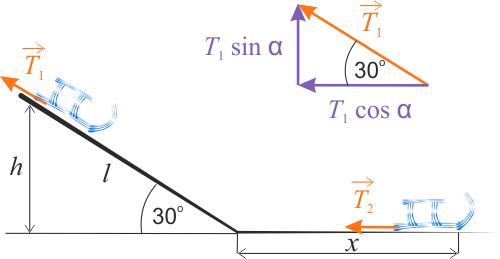
Rysunek


Na podstawie rysunku możemy zastąpić wielkość \(h\) wyrażeniem \(\displaystyle{\sin\alpha=\frac{h}{l}}\) i tak energia potencjalna wynosi

\(E_{pocz}=m\,g\,l\sin\alpha\)

Z drugiej strony możemy całkowitą pracę siły tarcia znaleźć, jako sumę pracy siły tarcia \(T_1\), podczas zsuwania się sanek ze zbocza oraz pracy siły tarcia \(T_2\), podczas jazdy na odcinku poziomym. Mamy:

\(W_T=W_{T_1}+W_{T_2}=-T_1l-T_2x\)

gdzie siły tarcia wynoszą: \(T_1=\mu mg\cos\alpha\) - składowa pozioma siły tarcia \(T_1\) oraz \(T_2=\mu mg\).
Ostatecznie otrzymujemy

\(W_{T_1}+W_{T_2}=E_{konc}-E_{pocz}\)

\(-T_1l-T_2x=0-mg\,l\sin\alpha\)
Po krótkich  \[-\mu mg\cos\alpha l-\mu mg\,x=0-mg\,l\sin\alpha\] \[\mu \cos\alpha \,l+\mu \,x=l\sin\alpha\] \[\mu \,x=l\sin\alpha-\mu\,l \cos\alpha\]  otrzymujemy

\(\displaystyle{x=\frac{l}{\mu}\sin\alpha-l\cos\alpha }\)

\(\displaystyle{x=\frac{12}{0,2}\cdot\sin 30^{\circ}-12\cdot \cos 30^{\circ} }\)

\(x=19,6\,\mathrm{m}\)

Odpowiedź

Na odcinku poziomym sanki przebędą drogę \(19,6\,\mathrm{m}\).