Zadanie 4.4.2.2
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.2 Trening
  5. Zadanie 4.4.2.2

 Zadanie 4.4.2.2

Kocek zsuwający sie z klina
Klin o masie \(3\mathrm{kg}\) wysokości \(1\mathrm{m}\) i długości podstawy \(2\mathrm{m}\) spoczywał na doskonale gładkim stole. Na jego nachylonej powierzchni położono klocek o masie \(2\mathrm{kg}\), który zaczął się zsuwać bez tarcia. Znajdź prędkość klina i klocka po jego zsunięciu się z klina.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
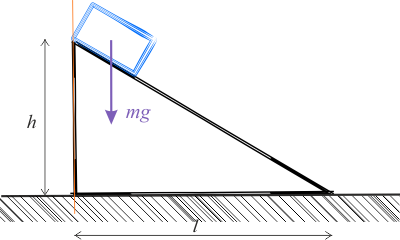
- masa klina \(M=3\,\mathrm{kg}\),
- masa klocka \(m=2\,\mathrm{kg}\),
- wysokość klina \(h=1\,\mathrm{m}\),
- długość podstawy klina \(l=2\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- końcowa prędkość klocka \(v_1\),
- końcowa prędkość klina \(v_2\).

Odpowiedź

Końcowa prędkość klocka wynosi \(\displaystyle{v_1= 3,75\,\mathrm{\frac{m}{s}} }\), a klina \(\displaystyle{v_2= 2,5\,\mathrm{\frac{m}{s}} }\).

Polecenie

Poniżej pokazane są dwa stwierdzenia dotyczące analizy sytuacji przedstawionej w zadaniu. Wybierz te, które uważasz za prawidłowe.

Stwierdzenie 1 z 2

Podczas zsuwania się klocka siłami zewnętrznymi w układzie są: siła ciężkości klocka i klina oraz siła reakcji podłoża działająca na podstawę klina.

Odpowiedź prawidłowa

Stwierdzenie 2 z 2

Po zsunięciu się klocka z klina siłami zewnętrznymi są: siły grawitacji oraz siły reakcji podłoża działająca na klin i klocek.

Odpowiedź prawidłowa

Mamy układ dwóch ciał oddziaływujących wzajemnie i na który działają siły zewnętrzne. Podczas zsuwania się klocka, siłami zewnętrznymi w układzie są: siła ciężkości klocka i klina oraz siła reakcji podłoża działająca na podstawę klina. Po zsunięciu się klocka z klina siłami zewnętrznymi są: siły grawitacji oraz siły reakcji podłoża działająca na klin i klocek. O siłach tych możemy powiedzieć, że:
- ponieważ w układzie w kierunku poziomym nie działają żadne siły zewnętrzne, to, dla tego kierunku, możemy stosować zasadę zachowania pędu,
- ponieważ w układzie działają jedynie niezrównoważone siły zachowawcze (nie ma np. siły tarcia), możemy stosować zasadę zachowania energii mechanicznej.

Polecenie

Oblicz wartość prędkości końcowej klocka \(v_1\) i klina \(v_2\). Wybierz jeden prawidłowy zestaw wartości, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{v_1= 3\,\mathrm{\frac{m}{s}} }\)
\(\displaystyle{v_2= 2\,\mathrm{\frac{m}{s}} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{v_1= 3,75\,\mathrm{\frac{m}{s}} }\)
\(\displaystyle{v_2= 2,5\,\mathrm{\frac{m}{s}} }\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{v_1= 2,5\,\mathrm{\frac{m}{s}} }\)
\(\displaystyle{v_2= 3\,\mathrm{\frac{m}{s}} }\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{v_1= 2\,\mathrm{\frac{m}{s}} }\)
\(\displaystyle{v_2= 3\,\mathrm{\frac{m}{s}} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

W chwili początkowej obydwa ciała są w spoczynku. Energia mechaniczna układu jest równa energii potencjalnej klocka (przy założeniu, że zero energii potencjalnej jest na poziomie powierzchni Ziemi), która wynosi:

\(E_p=mgh\)
Rysunek

Ponieważ nie ma tarcia między klockiem a klinem, energia mechaniczna układu jest zachowana. Po zsunięciu się klocka, jest ona równa sumie energii kinetycznej klocka i klina. Oznaczając wartości prędkości klocka i klina odpowiednio \(v_1\) i \(v_2\), mamy:

\(\displaystyle{mgh=\frac{mv_1^2}{2}+\frac{Mv_2^2}{2} }\)
Rysunek

Stosując zasadę zachowania pędu układu dla kierunku poziomego, dla chwili początkowej i po zsunięciu się klocka, mamy:

\(\sum p_x=0=mv_1+M(-v_2)\)
Po przekształceniach otrzymujemy

\(\displaystyle{v_1=\frac{M}{m}v_2 }\)

Otrzymaną wartość wstawiamy do równania opisującego zachowanie energii mechanicznej układu \(2gh=v_1^2+v_2^2\) i po  \[\displaystyle{2gh=\left ( \frac{M}{m}v_2\right )^2+v_2^2}\] \[\displaystyle{2gh=v_2^2\,\left ( \frac{M^2}{m^2}+1\right )}\] \[\displaystyle{2gh=v_2^2\,\left ( \frac{M^2+m^2}{m^2}\right )}\] \[\displaystyle{v_2^2=\frac{2gh\,m^2}{M^2+m^2} }\] \[\displaystyle{v_2=\sqrt{\frac{2gh\,m^2}{M^2+m^2}} }\]  mamy:

\(\displaystyle{v_2=m\sqrt{\frac{2gh}{M^2+m^2}} }\)
Po podstawieniu wartości liczbowych otrzymujemy:

\(\displaystyle{v_2=2\sqrt{\frac{2\cdot 10\cdot 1}{3^2+2^2}}=2,5 }\)   \(\displaystyle{\left [ \mathrm{kg\sqrt{\frac{\frac{m}{s^2}\cdot m}{kg^2}}}=\sqrt{\frac{m^2}{s^2}}=\frac{m}{s} \right ] }\)

\(\displaystyle{v_2=2,5\,\mathrm{\frac{m}{s}} }\)

Wartość prędkości końcowej klocka wynosi \(v_1\)

\(\displaystyle{v_1=\frac{3}{2}\cdot 2,5 }\)

\(\displaystyle{v_1= 3,75\,\mathrm{\frac{m}{s}} }\)

Odpowiedź

Końcowa prędkość klocka wynosi \(\displaystyle{v_1= 3,75\,\mathrm{\frac{m}{s}} }\), a klina \(\displaystyle{v_2= 2,5\,\mathrm{\frac{m}{s}} }\).