Zadanie 4.4.2.4
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.2 Trening
  5. Zadanie 4.4.2.4

 Zadanie 4.4.2.4

Skok z poruszającej się platformy
Dwie platformy poruszają się, w tym samym kierunku, po równoległych torach z prędkościami \(\displaystyle{v_1=4\,\mathrm{\frac{m}{s}}}\) i \(\displaystyle{v_2=6\,\mathrm{\frac{m}{s}}}\). Na wolniejszej platformie stoi człowiek o masie \(m=75\,\mathrm{kg}\). W pewnej chwili przeskakuje on na szybszą platformę w taki sposób, że prędkość wolniejszej spada do \(\displaystyle{\frac{1}{2}\,v_1 }\). Jaka będzie prędkość szybszej platformy po wylądowaniu człowieka? Obie platformy mają jednakowe masy, po \(M=100\,\mathrm{kg}\) każda.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa platform \(M=100\,\mathrm{kg}\),
- masa człowieka \(m=75\,\mathrm{kg}\),
- prędkość wolniejszej platformy \(\displaystyle{v_1=4\,\mathrm{\frac{m}{s}}}\),
- prędkość szybszej platformy \(\displaystyle{v_2=6\,\mathrm{\frac{m}{s}}}\),
- prędkość wolniejszej platformy po przeskoczeniu człowieka na szybszą \(\displaystyle{u_1=\frac{v_1}{2}=2\,\mathrm{\frac{m}{s}}}\).

Szukane:
- prędkość szybszej platformy po wylądowaniu człowieka \(u_2\).

Odpowiedź

Prędkość szybszej platformy po wylądowaniu człowieka wynosi \(\displaystyle{u_2=6,3\,\mathrm{\frac{m}{s}} }\).

Polecenie

Zastanów się, z jakich praw można skorzystać w przedstawionej sytuacji. Wybierz prawidłowe stwierdzenia, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

Można skorzystać z zasady zachowania pędu i nie można zastosować zasady zachowania energii.

Odpowiedź prawidłowa

Wybór 2 z 4

Można skorzystać z zasady zachowania pędu i można zastosować zasady zachowania energii.

Odpowiedź nieprawidłowa

Wybór 3 z 4

Nie można skorzystać z zasady zachowania pędu i nie można zastosować zasady zachowania energii.

Odpowiedź nieprawidłowa

Wybór 4 z 4

Nie można skorzystać z zasady zachowania pędu i można zastosować zasady zachowania energii.

Odpowiedź nieprawidłowa

Wyjaśnienie

Mamy układ trzech ciał, na który w płaszczyźnie ich ruchu (tj. w płaszczyźnie poziomej) nie działają żadne siły zewnętrzne (zakładamy, że tarcie i opór powietrza możemy pominąć), dlatego do opisu zdarzenia możemy zastosować zasadę zachowania pędu. Nie można natomiast stosować zasady zachowania energii mechanicznej ponieważ podczas przeskakiwania człowieka z platformy na platformę, część energii mechanicznej układu (tj. energii kinetycznej ruchu ciał) zamienia się na energię wewnętrzną. Zamiana energii mechanicznej na cieplną, dokonuje się podczas wyrównywania się prędkości drugiej platformy i człowieka, który na nią skacze. To wyrównywanie się prędkości możliwe jest dzięki pracy siły tarcia.

Polecenie

Wyznacz wartość prędkości szybszej platformy po wylądowaniu człowieka. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{u_2=6,3\,\mathrm{\frac{m}{s}}}\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(\displaystyle{u_2=7,4\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{u_2=8\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{u_2=10\,\mathrm{\frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Rzowiązanie

Sytuację w chwili tuż przed przeskoczeniem człowieka z jednej platformy na drugą i w chwili tuż po skoku, przedstawiono odpowiednio na poniższym rysunku. Założono, że platformy poruszają się wzdłuż osi \(x\). Oś \(x\) jest skierowana zgodnie z kierunkiem ruchu platform i stojącego na jednej z nich człowieka. 

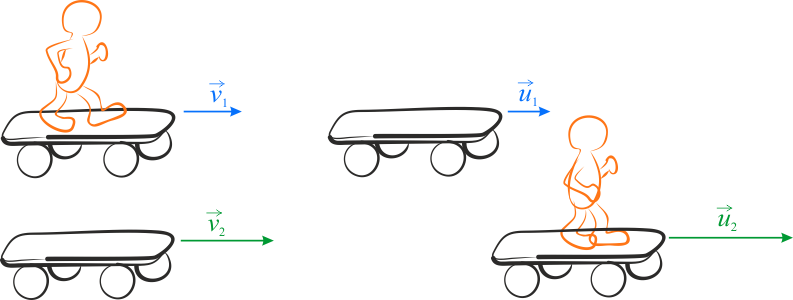
Rysunek


Z zasady zachowania pędu (dla kierunku \(x\)) mamy, że:

\(\sum p_x=(m+M)v_1+Mv_2=Mu_1+(m+M)u_2 \)

Z powyższego równania otrzymujemy:

\(\displaystyle{u_2=\frac{(m+M)v_1+Mv_2-Mu_1}{m+M} }\)

\(\displaystyle{u_2=\frac{(75+100)\cdot 4+100\cdot 6-100\cdot 2}{75+100} }\)

\(\displaystyle{u_2=6,3\,\mathrm{\frac{m}{s}} }\)
 Rozwiązaniem zadania jest wartość \(u_2>v_2\), czyli prędkość człowieka w chwili wylądowania na platformie musiała być większa od \(u_2\). Właśnie podczas wyrównywania się prędkości platformy i człowieka (człowiek przez krótki czas ślizga się aż do całkowitego zatrzymania) działa siła tarcia, która zamienia energię mechaniczną na cieplną. 

Odpowiedź

Prędkość szybszej platformy po wylądowaniu człowieka wynosi \(\displaystyle{u_2=6,3\,\mathrm{\frac{m}{s}} }\).