Zadanie 4.4.2.6
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.2 Trening
  5. Zadanie 4.4.2.6

 Zadanie 4.4.2.6

Zderzenie dwóch kul
Kula \(A\) o masie \(m_a=2\,\mathrm{kg}\) i prędkości \(\displaystyle{v=2\,\mathrm{\frac{m}{s}} }\) uderza centralnie i sprężyście w kulę \(B\) o masie \(m_b\). Jaką masę powinna mieć kula \(B\), aby po zderzeniu prędkość kuli \(A\) wynosiła:
  1. \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}}}\),
  2. \(\displaystyle{v_{a2}=-1\,\mathrm{\frac{m}{s}}}\),
  3. \(\displaystyle{v_{a3}=0}\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa kulki \(A\) \(m_a=2\,\mathrm{kg}\),
- prędkość kulki \(A\) przed zderzeniem \(\displaystyle{v=2\,\mathrm{\frac{m}{s}} }\),
- prędkość kulki \(A\) po zderzeniu w przypadku pierwszym \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}} }\),
- prędkość kulki \(A\) po zderzeniu w przypadku drugim \(\displaystyle{v_{a2}=-1\,\mathrm{\frac{m}{s}} }\),
- prędkość kulki \(A\) po zderzeniu w przypadku trzecim \(\displaystyle{v_{a3}=0 }\),

Szukane:
- masa kulki \(B\) \(m_b\).

Odpowiedź

W przypadku, gdy po zderzeniu prędkość kuli \(A\) wynosi \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}}}\), jej masa ma wartość \(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\). W kolejnym przypadku mamy \(\displaystyle{v_{a2}=-1\,\mathrm{\frac{m}{s}}}\) oraz \(\displaystyle{m_b=6\,\mathrm{kg} }\). W momencie kiedy kula \(A\) po zderzeniu zatrzyma się, obie kule mają tą samą masę \(\displaystyle{m_a=m_b=2\,\mathrm{kg} }\).

Polecenie

W pierwszym etapie rozwiązania wyprowadź wzór, pozwalający obliczyć masę kuli \(B\). Wybierz jedno prawidłowe równanie, wśród trzech przedstawionych poniżej.

Wybór 1 z 3

\(\displaystyle{m_b=\frac{v-v_a}{m_av} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 3

\(\displaystyle{m_b=m_a\frac{v-v_a}{v+v_a} }\)

Odpowiedź prawidłowa

Wybór 3 z 3

\(\displaystyle{m_b=\frac{m_a}{v+v_a} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Przed zderzeniem kluka \(A\) ma prędkość \(v\), zaś kula \(B\) nie porusza się.

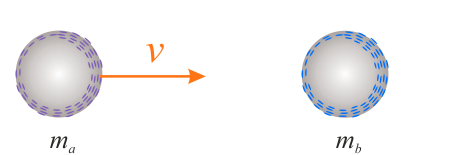
Rysunek


Po zderzeniu kule mogą poruszać się z prędkościami odpowiednio \(v_a\) oraz \(v_b\).

Rysunek


Z zasady zachowania pędu otrzymujemy

\(m_a\vec{v}=m_a\vec{v}_a+m_b\vec{v}_b\)

Zakładamy, że po zderzeniu obie kulki poruszają się w tym samym kierunku. Wiemy również, że zderzenie było zderzeniem sprężystym, a więc obowiązuje również zasada zachowania energii kinetycznej.

\(\displaystyle{\frac{m_av^2}{2}=\frac{m_av_a^2}{2}+\frac{m_bv_b^2}{2} }\)

Po przekształceniach otrzymujemy

\(\begin{eqnarray} \begin{cases} m_bv_b &=m_av-m_av_a\\ m_bv_b^2 &=m_av^2-m_av_a^2 \end{cases} \end{eqnarray} \)

Po podzieleniu stronami równania drugiego przez pierwsze, mamy:

\(\displaystyle{v_b=\frac{v^2-v_a^2}{v-v_a}=\frac{(v-v_a)(v+v_a)}{v-v_a} }\)

\(v_b=v+v_a\)

Z równania pierwszego otrzymujemy
\(\displaystyle{m_b=m_a\frac{v-v_a}{v_b} }\)

\(\displaystyle{m_b=m_a\frac{v-v_a}{v+v_a} }\)

Polecenie

Dla prędkości \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}}}\) oblicz masę kuli \(B\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(\displaystyle{m_b=1\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{m_b=2\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{m_b=6\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Po podstawieniu do wzoru \(\displaystyle{m_b=m_a\frac{v-v_a}{v+v_a} }\), otrzymujemy

\(\displaystyle{m_b=2\cdot\frac{2-1}{2+1}=\frac{2}{3} }\)

\(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\)

Komentarz:
Obie kule poruszają się w tym samym kierunku.
Masa kuli \(A\) wynosi \(m_a=2\,\mathrm{kg}\), prędkość \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}}}\).
Masa kuli \(B\) wynosi: \(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\), prędkość \(\displaystyle{v_{b1}=3\,\mathrm{\frac{m}{s}}}\).

Rysunek

Polecenie

Dla prędkości \(\displaystyle{v_{a1}=-1\,\mathrm{\frac{m}{s}}}\) oblicz masę kuli \(B\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{m_b=1\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{m_b=2\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{m_b=6\,\mathrm{kg} }\)

Odpowiedź prawidłowa

Rozwiązanie

Po podstawieniu do wzoru \(\displaystyle{m_b=m_a\frac{v-v_a}{v+v_a} }\), otrzymujemy

\(\displaystyle{m_b=2\cdot\frac{2-(-1)}{2-1}=6 }\)

\(\displaystyle{m_b=6\,\mathrm{kg} }\)

Komentarz:
Obie kule poruszają się w przeciwnych kierunkach z prędkościami o tej samej wartości.
Masa kuli \(A\) wynosi \(m_a=2\,\mathrm{kg}\), prędkość \(\displaystyle{v_{a1}=-1\,\mathrm{\frac{m}{s}}}\).
Masa kuli \(B\) wynosi: \(\displaystyle{m_b=6\,\mathrm{kg} }\), prędkość \(\displaystyle{v_{b1}=1\,\mathrm{\frac{m}{s}}}\).

Rysunek

Polecenie

Dla prędkości \(\displaystyle{v_{a1}=0}\) oblicz masę kuli \(B\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{m_b=1\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{m_b=2\,\mathrm{kg} }\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(\displaystyle{m_b=6\,\mathrm{kg} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Po podstawieniu do wzoru \(\displaystyle{m_b=m_a\frac{v-v_a}{v+v_a} }\), otrzymujemy

\(\displaystyle{m_b=2\cdot\frac{2-0}{2+0}=2 }\)

\(\displaystyle{m_b=2\,\mathrm{kg} }\)

Komentarz:
Kula \(A\) zatrzymała się, natomiast kula \(B\) porusza się w tym samym kierunki i prędkością, co przed zderzeniem kula \(A\).
Masa kuli \(A\) wynosi \(m_a=2\,\mathrm{kg}\), prędkość \(\displaystyle{v_{a1}=0 }\).
Masa kuli \(B\) wynosi: \(\displaystyle{m_b=2\,\mathrm{kg} }\), prędkość \(\displaystyle{v_{b1}=2\,\mathrm{\frac{m}{s}}}\).

Rysunek

Po kliknięciu w przycisk  Eksperyment otworzy się strona z filmem i wyjaśnieniem zderzeń centralnych.

Odpowiedź

W przypadku, gdy po zderzeniu prędkość kuli \(A\) wynosi \(\displaystyle{v_{a1}=1\,\mathrm{\frac{m}{s}}}\), jej masa ma wartość \(\displaystyle{m_b=\frac{2}{3}\,\mathrm{kg} }\). W kolejnym przypadku mamy \(\displaystyle{v_{a2}=-1\,\mathrm{\frac{m}{s}}}\) oraz \(\displaystyle{m_b=6\,\mathrm{kg} }\). W momencie kiedy kula \(A\) po zderzeniu zatrzyma się, obie kule mają tą samą masę \(\displaystyle{m_a=m_b=2\,\mathrm{kg} }\).