Zadanie 4.5.2.2
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.5. Pole grawitacyjne
  4. 4.5.2 Trening
  5. Zadanie 4.5.2.2

 Zadanie 4.5.2.2

Tunel przez Ziemię
Wyobraź sobie przewierconą przez środek na wylot Ziemię. Oblicz, jak zmienia się przyspieszenie grawitacyjne w zależności od odległości od środka Ziemi. Załóż, że znasz promień Ziemi oraz przyspieszenie grawitacyjne na jej powierzchni.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
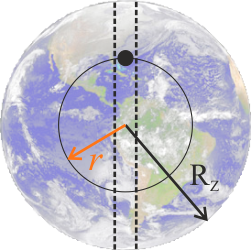
- promień Ziemi \(R_Z\),
- przyspieszenie ziemskie \(\displaystyle{g}\).

Szukane:
- przyspieszenie grawitacyjne \(a_g(r)\).

Odpowiedź

Zmianę przyspieszenia grawitacyjne w zależności od odległości od środka Ziemi \(r\) opisuje zależność \(\displaystyle{a_g(r)=\frac{g}{R_Z}r }\).

Polecenie

Wyznacz zależność opisującą natężenie pola grawitacyjnego (przyspieszenie grawitacyjne). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{a_g(r)=G\frac{g}{R_Z^2}r }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{a_g(r)=\frac{R_Z}{2g}r }\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{a_g(r)=\frac{g}{R_Z}r }\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(\displaystyle{a_g(r)=\frac{G}{r}R_Z^2 }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Siła grawitacji działająca na masę próbną \(m\), znajdującą się w odległości \(r\) od środka Ziemi, opisuje zależność

\(\displaystyle{F_g=-G\frac{M'_Zm}{r^2} }\)

Masa \(M'_Z\) to część całkowitej masy Ziemi wyciętej przez sferę o promieniu \(r\)

\(\displaystyle{\frac{M'_Z}{M_Z}=\frac{\frac{4}{3}\pi r^3}{\frac{4}{3}\pi R_Z^3}=\frac{r^3}{R_Z^3} }\)

\(\displaystyle{M'_Z=M_Z\frac{r^3}{R_Z^3} }\)

Rysunek


Natężenie pola grawitacyjnego, czyli przyspieszenie grawitacyjne wyniesie więc

\(\displaystyle{a_g\cong \gamma=\frac{F_g}{m}=G\frac{M'_Z}{r^2} }\)

\(\displaystyle{a_g=G\frac{1}{r^2}M_Z\frac{r^3}{R_Z^3}=G\frac{M_Z}{R_Z^3}r }\)

Pamiętając, że z definicji siły grawitacyjnej na powierzchni Ziemi wynika, że

\(\displaystyle{F_g=G\frac{M_zm}{R_Z^2}=gm }\)

\(\displaystyle{g=G\frac{M_z}{R_Z^2} }\)

Podstawiając ten wniosek do poprzedniego równania otrzymujemy

\(\displaystyle{a_g\cong \gamma=\frac{g}{R_Z}r }\)

Przyspieszenie grawitacyjne maleje liniowo do środka Ziemi.

Odpowiedź

Zmianę przyspieszenia grawitacyjne w zależności od odległości od środka Ziemi \(r\) opisuje zależność \(\displaystyle{a_g(r)=\frac{g}{R_Z}r }\).