Zadanie 4.5.2.3
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.5. Pole grawitacyjne
  4. 4.5.2 Trening
  5. Zadanie 4.5.2.3

 Zadanie 4.5.2.3

Zmiana przyspieszenia grawitacyjnego
Księżyc okrążając Ziemię znajduje się raz z jednej, raz z drugiej strony. Powoduje to, że przyspieszenie grawitacyjne na powierzchni Ziemi ulega pewnym zmianom. Oblicz amplitudę tych zmian wiedząc, że odległość Ziemia Księżyc wynosi \(r_{ZK}=384,4\cdot 10^6\,\mathrm{m} \), jego masa \(M_k=7,35\cdot 10^{22}\,\mathrm{kg}\), natomiast średni promień Ziemi \(R_Z=6371\,\mathrm{km} \). Jaki procent przyspieszenia grawitacyjnego na powierzchni Ziemi stanowi ta amplituda? Stała grawitacji wynosi \(\displaystyle{G=6,67\cdot 10^{-11}\,\mathrm{\frac{m^3}{kg\,s^2}} }\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- odległość Ziemia Księżyc \(r_{ZK}=3,844\cdot 10^8\,\mathrm{m} \),
- masa Księżyca \(M_K=7,35\cdot 10^{22}\,\mathrm{kg}\),
- średni promień Ziemi \(R_Z=6371\,\mathrm{km}=6,371\cdot 10^6\,\mathrm{m}  \),
- stała grawitacyjna \(\displaystyle{G=6,67\cdot 10^{-11}\,\mathrm{\frac{m^3}{kg\,s^2}} }\).

Szukane:
- zmiana przyspieszenia grawitacyjnego \(\Delta g\).

Odpowiedź

Amplituda zmian przyspieszenie grawitacyjne na powierzchni Ziemi wynosi \(\displaystyle{\Delta g=6,64\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\), co stanowi \(0,007\%\).

Polecenie

Wybierz, wśród dwóch przedstawionych poniżej stwierdzenie, które nakieruje Cię na przedstawiony tok rozwiązywania zadania.

Stwierdzenie 1 z 2

Zmiana natężenia pola grawitacyjnego Księżyca będzie odpowiedzialna za zmiany wypadkowego przyspieszenia grawitacyjnego na powierzchni Ziemi.

Odpowiedź prawidłowa

Stwierdzenie 2 z 2

Zmiany ziemskiego przyspieszenia grawitacyjnego związanego z ruchem Księżyca po orbicie wywołują pływy oceaniczne.

Odpowiedź nieprawidłowa

Polecenie

Wyznacz wartość zmiany przyspieszenia grawitacyjnego na powierzchni Ziemi. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{\Delta g=9,8\cdot 10^{-3}\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{\Delta g=6,64\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{\Delta g=8,64\cdot 10^{-2}\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{\Delta g=3,32\cdot 10^{-6}\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa
Wartość ta stanowi

\(\displaystyle{\frac{\Delta g}{g}=\frac{6,64\cdot 10^{-5}}{9,8}=6,78\cdot 10^{-5}\cong 0,007\%}\)

przyspieszenia grawitacyjnego na powierzchni Ziemi.

Rozwiązanie

Przyspieszenie grawitacyjne Księżyca, działające na masę \(m\), określa zależność

\(\displaystyle{a_{gK}=\frac{F_{gK}}{m} }\)

Siłę grawitacji zapisujemy dla dwóch przypadków

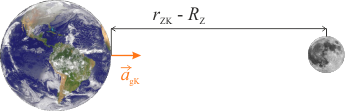
Rysunek


\(\displaystyle{F_{K1}=G\frac{M_Km}{(r_{ZK}- R_Z)^2} }\)

Rysunek


\(\displaystyle{F_{K2}=G\frac{M_Km}{(r_{ZK}+ R_Z)^2} }\)

Po podstawieniu siły do pierwszego wzoru mamy

\(\displaystyle{a_{gK1}=G\frac{M_K}{(r_{ZK}- R_Z)^2} }\)   oraz   \(\displaystyle{a_{gK2}=G\frac{M_K}{(r_{ZK}+ R_Z)^2} }\)

\(\displaystyle{a_{gK1}=G\frac{7,35\cdot 10^{22}}{(3,844\cdot 10^8\pm 6,371\cdot 10^6)^2} }\)

\(\displaystyle{a_{gK1}=3,21\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\)   oraz   \(\displaystyle{a_{gK2}=3,43\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\)

Amplituda przyspieszenia jest równa sumie tych wartości

\(\displaystyle{\Delta g=a_{gK1}+a_{gK2}=6,64\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\)

Wartość ta stanowi

\(\displaystyle{\frac{\Delta g}{g}=\frac{6,64\cdot 10^{-5}}{9,8}=6,78\cdot 10^{-5}\cong 0,007\%}\)

Co dla człowieka jest zupełnie niezauważalną wartością.

Odpowiedź

Amplituda zmian przyspieszenie grawitacyjne na powierzchni Ziemi wynosi \(\displaystyle{\Delta g=6,64\cdot 10^{-5}\,\mathrm{\frac{m}{s^2}} }\), co stanowi \(0,007\%\).