Zadanie 5.1.1.2
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.1. Środek masy
  4. 5.1.1 Nauka
  5. Zadanie 5.1.1.2

 Zadanie 5.1.1.2

Środek ciężkości ciał, na które działa siła
Trzy ciała o masach \(m_1=4\,\mathrm{kg }\), \(m_2=8\,\mathrm{kg }\) oraz \(m_3=4\,\mathrm{kg }\) umieszczono na płaszczyźnie. W chwili \(t=0\) ciała te są w spoczynku, a ich położenie wynosi odpowiednio: \((-2,2)\,\mathrm{m}\), \((4,1)\,\mathrm{m}\) oraz \((-3,0)\,\mathrm{m}\). Na każde z tych ciał działa siła: \(\vec{F}_1=-F_1\,\hat{x}\), \(F_1=16\,\mathrm{N}\); \(\vec{F}_2=F_2\,\hat{y}\), \(F_2=16\,\mathrm{N}\); \(\vec{F}_3=F_3\,\hat{x}\), \(F_3=8\,\mathrm{N}\). Znajdź położenie środka masy w chwili \(t=2\,\mathrm{s}\).

 Wskazówka teoretyczna

 Teoria - środek masy układu ciał
Wektor położenia środka masy układu \(N\) punktów materialnych definiujemy jako

\(\displaystyle{\vec{r}_s=\frac{1}{M}\sum_{i=1}^{N}m_i \vec{r}_i^2 }\),

gdzie \(m_i\) i \(\vec{r}_i^2\) to odpowiednio masa i wektor położenia i-tego punktu materialnego, a \(M\) jest masą całego układu. 
Powyższą definicję możemy odnieść do ciał o skończonych rozmiarach pod warunkiem, że ciało podzielimy na bardzo małe (w porównaniu z rozmiarami ciała) obszary, które będziemy traktowali, jako punkty mające masę tego obszaru. Można pokazać, że środek mas ciał symetrycznych leży na osiach lub w środku symetrii – np. środek masy jednorodnej kuli leży w środku kuli, środek masy jednorodnej belki leży w środku jej długości itp. Jeżeli, z czym często spotykamy się w zadaniach, mamy układ ciał o skończonych rozmiarach, to środek masy tego całego układu wyznaczamy, traktując ciała układu jako punkty materialne, znajdujące się w położeniach ich środków mas.  

Komentarz: Środek masy ciała może leżeć poza ciałem, np. środek masy jednorodnego pierścienia będzie położony w jego środku.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa pierwszego ciała \(m_1=4\,\mathrm{kg }\),
- masa drugiego ciała \(m_2=8\,\mathrm{kg }\),
- masa trzeciego ciała \(m_3=4\,\mathrm{kg }\)
- położenia kolejno trzech ciał w chwili \(t=0\): \((-2,2)\,\mathrm{m}\), \((4,1)\,\mathrm{m}\) oraz \((-3,0)\,\mathrm{m}\),
- siła działająca na pierwsze ciało \(\vec{F}_1=-F_1\,\hat{x}\), \(F_1=16\,\mathrm{N}\),
- siła działająca na drugie ciało \(\vec{F}_2=F_2\,\hat{y}\), \(F_2=16\,\mathrm{N}\),
- siła działająca na trzecie ciało \(\vec{F}_3=F_3\,\hat{x}\), \(F_3=8\,\mathrm{N}\).

Szukane:
- położenie środka masy w chwili \(t=2\,\mathrm{s}\): \(r_s\).

Analiza sytuacji

Na rysunku przedstawiono siły działające na trzy ciał w chwili \(t=0\).

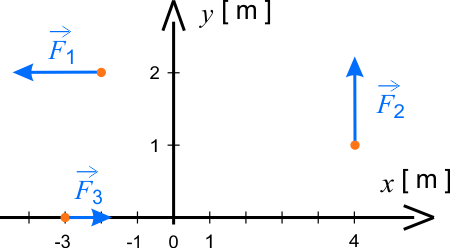
Rysunek


Wektor położenia środka masy układu ciał w chwili \(t=0\), zgodnie z definicją, wynosi

\(\displaystyle{\vec{r}_{0s}=\frac{m_1\vec{r}_{01}+m_2\vec{r}_{02}+m_3\vec{r}_{03}}{m} }\)

gdzie \(\vec{r}_{01}\), \(\vec{r}_{02}\), \(\vec{r}_{03}\) oznaczają wektory położenia ciała w chwili \(t=0\), a \(m=m_1+m_2+m_3\) jest masą układu trzech ciał.

Jeżeli w chwili początkowej ciała były w spoczynku, to również środek masy był w spoczynku. Ruch środka masy odbywa się pod wpływem siły \(\vec{F}\), która jest sumą sił działających na wszystkie ciała układu.

\(\vec{F}=\vec{F}_1+\vec{F}_2+\vec{F}_3\)

Pod wpływem tej siły \(\vec{F}\) środek masy uzyskuje przyspieszenie \(\vec{a}_s\) zgodnie ze wzorem:

\(\vec{F}=m\vec{a}_s\),

który jest równaniem ruchu środka masy danego układu punktów. Z powyższej zależności obliczymy \(\vec{a}_s\).

Prędkość środka masy obliczamy z równania \(\displaystyle{\vec{v}_s=\int \vec{a}_s\mathrm{d}t }\), a położenie środka masy \(\displaystyle{\vec{r}_s=\int \vec{v}_s\mathrm{d}t }\).

Rozwiązanie - obliczenia

Wektor położenia środka masy układu ciał w chwili \(t=0\) wynosi

- współrzędna \(x\)-owa: \(\displaystyle{\vec{r}_{0sx}=\frac{4\cdot (-2)+8\cdot 4+4\cdot (-3)}{4+8+4}=\frac{3}{4} }\)

- współrzędna \(y\)-owa: \(\displaystyle{\vec{r}_{0sy}=\frac{4\cdot 2 +8\cdot 1+4\cdot 0}{4+8+4}=1 }\)

\(\displaystyle{\vec{r}_{0s}=\left (\frac{3}{4},1 \right )\,\mathrm{m} }\)

Siła, pod wpływem której środek masy uzyskuje przyspieszenie, wynosi:

\(\vec{F}=-F_1\hat{x}+F_2\hat{y}+F_3\hat{x}=(F_3-F_1)\hat{x}+F_2\hat{y} \)

\(\vec{F}=(8-16,16)=(-8,16)\,\mathrm{N} \)

Przyspieszenie środka masy wynosi
\(\displaystyle{\vec{a}_s=\frac{\vec{F}}{m}=\frac{(-8,16)}{16} }\)

\(\displaystyle{\vec{a}_s=\left ( -\frac{1}{2},1\right )\,\mathrm{\frac{m}{s^2}} }\)

Prędkość środka masy w chwili \(t\) wynosi

- współrzędna \(x\)-owa: \(\displaystyle{\vec{v}_{sx}=\int \left ( -\frac{1}{2}\right )\, \mathrm{d}t=-\frac{1}{2}t }\)

- współrzędna \(y\)-owa: \(\displaystyle{\vec{v}_{sy}=\int 1\,\mathrm{d}t=t }\)

\(\displaystyle{\vec{v}_s=\int \vec{a}_s \mathrm{d}t=\left ( -\frac{1}{2}t,t\right )+\vec{C}_1 }\)

gdzie \(\vec{C}_1\) jest stałą (wektorową) całkowania. Stałą tą wyznaczymy z warunku takiego, że w chwili \(t=0\) prędkość środka masy wynosi zero.

\(\vec{v}_s(t=0)=\left ( 0,0\right )=\vec{C}_1\)

Położenie środka masy układu dane jest przez wektor wodzący środka masy

\(\displaystyle{\vec{r}_s=\int \vec{v}_s\,\mathrm{d}t=\int \left ( -\frac{1}{2}t,t\right )\,\mathrm{d}t }\)

\(\displaystyle{\vec{r}_s=\left ( -\frac{1}{4}t^2,\frac{1}{2}t^2\right )+\vec{C}_2 }\)

gdzie stałą \(\vec{C}_2\), podobnie jak poprzednio, wyznaczymy z warunku początkowego.

\(\displaystyle{\vec{r}_s(t=0)=\vec{r}_{0s}=\left ( \frac{3}{4},1\right )=\vec{C}_2 }\)

\(\displaystyle{\vec{r}_s=\left (\frac{3}{4} -\frac{1}{4}t^2,1+\frac{1}{2}t^2\right )\,\mathrm{m} }\)

Położenie środka masy w chwili \(t=2\,\mathrm{s}\) wynosi

\(\displaystyle{\vec{r}_s=\left (\frac{3}{4} -\frac{1}{4}\cdot 2^2,1+\frac{1}{2}\cdot 2^2\right ) }\)

\(\displaystyle{\vec{r}_s=\left (-\frac{1}{4},3\right )\,\mathrm{m} }\).

Odpowiedź

Położenie środka masy w chwili \(t=2\,\mathrm{s}\) wynosi \(\displaystyle{\vec{r}_s=\left (-\frac{1}{4},3\right )\,\mathrm{m} }\).