Zadanie 5.1.1.3
Środek masy półokręgu
Znajdź środek masy półokręgu o promieniu \(r\).
Wskazówka teoretyczna
Teoria - środek masy ciała
Wektor położenia środka masy ciała definiujemy jako
gdzie \(\vec{r}_i^2\) oznacza wektor położenia elementu masy \(\mathrm{d}m\), a \(M\) jest masą całkowitą ciała.
\(\displaystyle{\vec{r}_s=\frac{1}{M}\int_{M} \vec{r}\mathrm{d}m }\),
gdzie \(\vec{r}_i^2\) oznacza wektor położenia elementu masy \(\mathrm{d}m\), a \(M\) jest masą całkowitą ciała.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- promień półokręgu \(r\).
Szukane:
- środek masy półokręgu \(y_0\).
Analiza sytuacji
Dla danego ciała, współrzędne jego środka masy wyznaczamy obliczając następujące całki
\(\displaystyle{x_0=\frac{1}{M}\int_{M} x\,\mathrm{d}m }\), \(\displaystyle{y_0=\frac{1}{M}\int_{M} y\,\mathrm{d}m }\), \(\displaystyle{z_0=\frac{1}{M}\int_{M} z\,\mathrm{d}m }\),
gdzie \(M\) oznacza masę ciała, natomiast \(\mathrm{d}m\) jest masą nieskończenie małego elementu ciała, mającego współrzędne \(\left ( x,y,z\right )\).
W przypadku półokręgu (zakładamy, że grubość łuku jest zaniedbywalnie mała w porównaniu z jego promieniem) element masy \(\mathrm{d}m\) można zapisać następująco
\(\mathrm{d}m=\rho \mathrm{d}V=\rho S \mathrm{d}l\),
gdzie \(\rho\) jest gęstością materiału, z którego wykonano półokrąg, \(S\) polem jego przekroju poprzecznego, a \(\mathrm{d}l\) elementem długości łuku półokręgu.
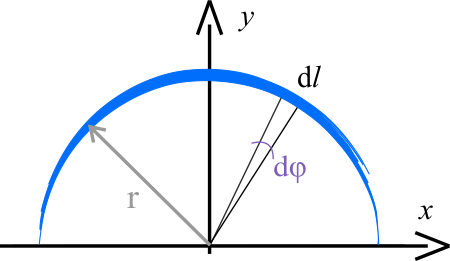
Elementem długości łuku półokręgu można przedstawić jako iloczyn \(r\,\mathrm{d}\varphi\), gdzie \(\mathrm{d}\varphi\) jest elementarnym kątem przedstawionym za pomocą miary łukowej. Rozważany element masy ma współrzędne:
\(x=r\cos\varphi\), \(y=r\sin\varphi\)
Współrzędnej \(x_0\) środka masy nie trzeba w tym przypadku liczyć, gdyż z symetrii ciała wynika, że jego środek masy musi leżeć na osi \(0Y\). Należy jedynie wyliczyć jego współrzędną \(y_0\).
Obliczenia
\(\displaystyle{y_0=\frac{1}{M}\int_{0}^{\pi} r\sin\varphi\,\mathrm{d}m }\)
\[\displaystyle{y_0=\frac{1}{M}\int_{0}^{\pi} r\sin\varphi\,\rho Sr\,\mathrm{d}\varphi }\] \[\displaystyle{y_0=\frac{r^2\rho S}{M}\int_{0}^{\pi} \sin\varphi\,\mathrm{d}\varphi }\] \[\displaystyle{y_0=\frac{r^2\rho S}{M}\left [-\cos\varphi\right ]_0^{\pi} }\] \[\displaystyle{y_0=\frac{r^2\rho S}{M}\left (-\cos\pi+\cos 0\right ) }\]
\(\displaystyle{y_0=\frac{2r^2\rho S}{M} }\)
Ostatecznie, wprowadzając wzór na masę całkowitą \(M=\pi r\rho S\), otrzymujemy:
\(\displaystyle{y_0=\frac{2}{\pi}r }\)
Odpowiedź
Środek masy półokręgu ma współrzędną \(\displaystyle{y_0=\frac{2}{\pi}r }\).
