Zadanie 5.1.2.2
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.1. Środek masy
  4. 5.1.2 Trening
  5. Zadanie 5.1.2.2

 Zadanie 5.1.2.2

Chłopiec na łyżwach ciągnie skrzynię
Na lodzie leży skrzynia o masie \(20\,\mathrm{kg}\), do której przywiązana jest lina o długości \(7\,\mathrm{m}\). Drugi koniec liny trzyma chłopiec stojący na łyżwach. Masa chłopca razem z łyżwami wynosi \(50\,\mathrm{kg}\). Tarcie pomiędzy skrzynią i lodem oraz łyżwami a lodem jest zaniedbywalnie małe. Za pomocą tej liny chłopiec przyciąga skrzynię do siebie. O ile przesunął się chłopiec do momentu przyciągnięcia skrzyni do siebie?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa skrzyni \(m=20\,\mathrm{kg}\),
- masa chłopca \(M=50\,\mathrm{kg}\),
- długość liny \(l=7\,\mathrm{m}\).

Szukane:
- odległość o jaką przesunął się chłopiec \(d\).

Odpowiedź

Końcowe położenie chłopca zmieni się o \(d=2\,\mathrm{m}\).

Polecenie

Jak zachowa się środek masy układu w opisanej sytuacji? Wybierz jedną prawidłową odpowiedź, spośród dwóch przedstawionych poniżej.

Wybór 1 z 2

Środek masy układu przesunie się w stronę cięższego obiektu.

Odpowiedź nieprawidłowa

Wybór 1 z 2

Środek masy układu nie zmieni swojego położenia.

Odpowiedź prawidłowa
Przy założeniu, że tarcie pomiędzy skrzynią i lodem oraz łyżwami a lodem jest zaniedbywalnie małe, w kierunku poziomym ani na chłopca, ani na skrzynię nie działa żadna siła zewnętrzna. W układzie działają jedynie siły wewnętrzne wzajemnego oddziaływania chłopca i skrzyni (poprzez linę). W takim przypadku środek masy układu chłopiec – skrzynia musi pozostać w tym samym miejscu, czyli przesuwanie się chłopca i skrzyni będzie tak, że środek masy nie będzie zmieniał swojego położenia.

Polecenie

Wyznacz odległość środka masy układu od chłopca. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x_s=0,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x_s=1\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(x_s=2\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(x_s=4\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Sytuację opisaną w zadaniu przedstawia rysunek. Na rysunku wprowadziliśmy jednowymiarowy układ współrzędnych z osią \(x\) skierowaną w prawo i mającą swój początek w miejscu początkowego położenia chłopca.

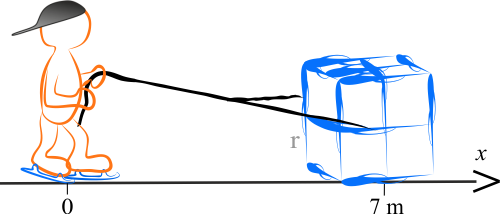
Rysunek


W układzie tym położenie środka masy tego układu znajduje się na osi \(x\) w punkcie o współrzędnej \(x_s\) i wynosi

\(\displaystyle{x_s=\frac{M\cdot 0+ml}{M+m}=\frac{ml}{M+m} }\)

\(\displaystyle{x_s=\frac{20\cdot 7}{20+50}=2\,\mathrm{m} }\)

Podczas przyciągania skrzyni przez chłopca środek masy układu chłopiec – skrzynia pozostaje w tym samym miejscu aż do momentu, gdy chłopiec zetknie się ze skrzynią, czyli końcowe położenie chłopca jest położeniem środka masy. Mamy więc:

\(d=2\,\mathrm{m}\)
 Fakt, że środek masy układu chłopiec–skrzynia pozostaje w tym samym miejscu, wynika z zasady zachowania pędu układu. Ponieważ w kierunku ruchu chłopca i skrzyni nie działają żadne siły zewnętrzne, pęd układu pozostaje stały. Ponieważ pęd układu jest tożsamy z pędem środka masy, wnioskujemy, że prędkość środka masy pozostaje stała. Ale skoro na początku środek masy spoczywał to w czasie ruchu układu musiał pozostać w tym samym miejscu. Spotkanie w każdym innym miejscu musiałoby zmienić położenie środka masy. 

Odpowiedź

Końcowe położenie chłopca zmieni się o \(d=2\,\mathrm{m}\).