Zadanie 5.1.2.4
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.1. Środek masy
  4. 5.1.2 Trening
  5. Zadanie 5.1.2.4

 Zadanie 5.1.2.4

Środek masy układu Ziemia - Słońce
Znajdź środek masy układu Ziemia - Słońce wiedząc, że odległość między środkami Ziemi i Słońca wynosi \(d=150\,\mathrm{mln\,km}\), masa Ziemi wynosi \(M_Z =6\cdot 10^{24}\,\mathrm{kg}\), a masa Słońca \(M_S=2\cdot 10^{30}\,\mathrm{kg}\). Załóż, że Ziemia i Słońce są jednorodnymi kulami.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- odległość między środkami Ziemi i Słońca \(d=150\,\mathrm{mln\,km}=1,5\cdot 10^{11}\,\mathrm{m}\),
- masa Ziemi \(M_Z =6\cdot 10^{24}\,\mathrm{kg}\),
- masa Słońca \(M_S=2\cdot 10^{30}\,\mathrm{kg}\).

Szukane:
- odległość środka masy układu Ziemia - Słońce od środka Słońca \(x_s\).

Odpowiedź

Położenie środka masy układu Ziemia - Słońce wynosi \(x_s=450\,\mathrm{km}\).

Polecenie

Wyznacz odległość środka masy układu Ziemia - Słońce od środka Słońca. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x_s=150\,\mathrm{km}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x_s=450\,\mathrm{km}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(x_s=1500\,\mathrm{km}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(x_s=4500\,\mathrm{km}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Z założenia, że Ziemia i Słońce są jednorodnymi kulami wynika, że ich środki masy pokrywają się z ich środkami geometrycznymi. Przy obliczaniu środka masy układu tych ciał, można je zastąpić ich środkami mas. Wyznaczenie środka masy układu Ziemia Słońce sprowadzimy w ten sposób do klasycznego wyznaczenia środka masy układu punktów materialnych.

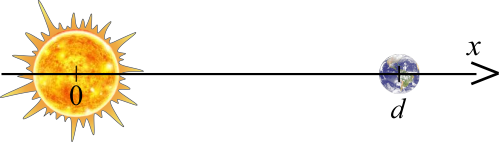
Rysunek


Oba ciała oraz położenia ich środków przedstawia rysunek w jednowymiarowym układzie współrzędnych osi \(x\) skierowanej w prawo, przy czym przyjęliśmy, że środek Słońca (środek jego masy) pokrywa się ze środkiem układu.

Korzystając z definicji położenia środka masy układu punktów materialnych, mamy:

\(\displaystyle{x_s=\frac{\sum m_i x_i}{m_i}=\frac{M_S\cdot 0+M_Z\cdot d}{M_S+M_Z} }\)

\(\displaystyle{x_s=\frac{6\cdot 10^{24}\cdot 1,5\cdot 10^{11}}{2\cdot 10^{30}+6\cdot 10^{24}}=4,5\cdot 10^5\,\mathrm{m} }\)

\(x_s=450\,\mathrm{km}\)

Jak widać środek masy układu Ziemia Słońce znajduje się wewnątrz Słońca blisko jego środka.

Odpowiedź

Położenie środka masy układu Ziemia - Słońce wynosi \(x_s=450\,\mathrm{km}\).