Zadanie 5.1.2.5
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.1. Środek masy
  4. 5.1.2 Trening
  5. Zadanie 5.1.2.5

 Zadanie 5.1.2.5

Środek masy wydrążonej kulii
Znajdź środek masy jednorodnej kuli o promieniu \(r_1=50\,\mathrm{cm}\), w której wnętrzu znajduje się kuliste wydrążenie o promieniu \(r_2=20\,\mathrm{cm}\), przy czym środek kuli mniejszej położony jest w punkcie o współrzędnych \(D=(-4,3)\,\mathrm{cm}\), a kuli większej \(S=(0,0)\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- promień dużej kuli \(r_1=50\,\mathrm{cm}\),
- promień małej kuli \(r_2=20\,\mathrm{cm}\),
- odległość mniejszej kuli od środka kuli większej \(x_0=-4\,\mathrm{cm}\) i \(y_0=3\,\mathrm{cm}\).

Szukane:
- środek masy kuli wydrążonej \(R_s=(x_1,y_1)\).

Odpowiedź

c

Polecenie

Wyznacz zależność pozwalającą na obliczenie współrzędnej \(x_1\) środka masy. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{x_1=-\frac{r_2^3}{r_1^3-r_2^3}\cdot x_0}\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(\displaystyle{x_1=\frac{r_2^3}{r_1^3-r_2^3}\cdot x_0}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{x_1=-\frac{r_2^3}{r_1^3}\cdot x_0}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{x_1=\frac{r_1^3-r_2^3}{r_2^3}\cdot x_0}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Pełna kula o promieniu \(r_1\) składa się z małej kuli o promieniu \(r_2\) i masie \(m_2\) oraz dużej kuli o promieniu \(r_1\) z wydrążeniem i masie \(m_1\).

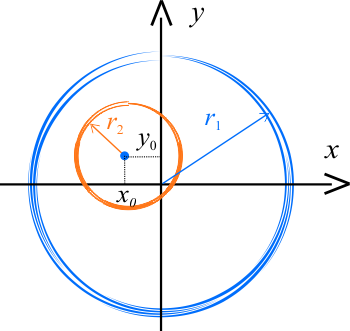
Rysunek


Dla pełnej kuli środek masy ma (w układzie współrzędnych pokazanym na rysunku) współrzędne

\(\displaystyle{x_s=0=\frac{x_1m_1+x_0m_2}{m_1+m_2} }\),    \(\displaystyle{y_s=\frac{y_1m_1+y_0m_2}{m_1+m_2} }\),    \(z_s=0\),

przy czym \((x_1,y_1)\) oznaczają współrzędne środka masy kuli z wydrążeniem, natomiast \((x_0,y_0)\) oznacza współrzędne środka masy małej kuli, którą usuwamy, tworząc wydrążenie.
Dla współrzędnej \(x_s\) mamy:

\(\displaystyle{0=\frac{x_1m_1+x_0\,m_2}{m_1+m_2} }\)

\(0=x_1m_1+x_0\,m_2\)

\(\displaystyle{x_1=-\frac{m_2}{m_1}x_0 }\)

Teraz wyznaczmy masę \(m_2\). Zakładamy, że gęstość materiału kuli wynosi \(\rho\), wtedy

\(\displaystyle{m_2=V_2\rho=\frac{4}{3}\pi r_2^3\rho }\)

Masa \(m_1\) równa jest różnicy masy całej pełnej kuli i wydrążenia.

\(\displaystyle{m_1=\frac{4}{3}\pi r_1^3\rho -\frac{4}{3}\pi r_2^3\rho=\frac{4}{3}\pi\rho\left (r_1^3-r_2^3\right ) }\)

Współrzędna środka masy wynosi

\(\displaystyle{x_1=-\frac{\frac{4}{3}\pi\rho r_2^3}{\frac{4}{3}\pi\rho\left (r_1^3-r_2^3\right )}x_0 }\)

\(\displaystyle{x_1=-\frac{r_2^3}{r_1^3-r_2^3}x_0 }\)

Polecenie

Oblicz współrzędne środka masy. Wybierz jedną prawidłową wartość, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(\displaystyle{r_s=\left (\frac{16}{21},-\frac{12}{21} \right)\,\mathrm{cm}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 2

\(\displaystyle{r_s=\left (\frac{32}{117},-\frac{24}{117} \right)\,\mathrm{cm}}\)

Odpowiedź prawidłowa

Rozwiązanie

Współrzędna \(x_1\) wynosi

\(\displaystyle{x_1=-\frac{20^3}{50^3-20^3}\cdot (-4) }\)

\(\displaystyle{x_1=\frac{32}{117}\,\mathrm{cm} }\)
Współrzędna \(y_1\) wynosi

\(\displaystyle{y_1=-\frac{20^3}{50^3-20^3}\cdot 3 }\)

\(\displaystyle{y_1=-\frac{24}{117}\,\mathrm{cm} }\)

Odpowiedź

Środek masy wydrążonej kuli ma współrzędne \(\displaystyle{r_s=\left (\frac{32}{117},-\frac{24}{117} \right)\,\mathrm{cm}}\).