Zadanie 5.2.2.6
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.2. Moment bezwładności
  4. 5.2.2 Trening
  5. Zadanie 5.2.2.6

 Zadanie 5.2.2.6

Tensor momentu bezwładności
Wyznacz tensor momentu bezwładności względem osi \(x\), \(y\), \(z\) dwóch ciał o masach \(m\) i \(3m\) leżących w odległości \(10\,\mathrm{cm}\) od siebie tak, że ich środek ciężkości ma współrzędne \((0,0,0)\).
Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
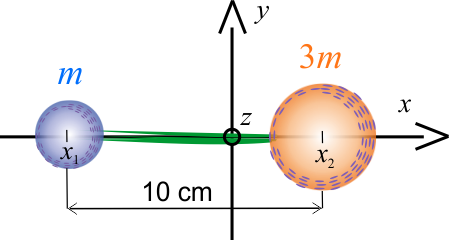
- masa ciała pierwszego \(3m\),
- masa ciała drugiego \(m\),
- odległość między połączonymi ciałami \(d=10\,\mathrm{cm}\),
- współrzędne środka ciężkości \((0,0,0)\).

Szukane:
- tensor momentu bezwładności \(\hat{I}\).

Odpowiedź

Tensor momentu bezwładności ma postać:

\(\hat{I}=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0,0075m & 0 \\ 0 & 0  & 0,0075m \end{bmatrix}\)

Polecenie

Wyznacz odległość \(x_1\) (powyższy rysunek) od środka ciężkość. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x_1=-15\,\mathrm{cm}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x_1=-10\,\mathrm{cm}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(x_1=-8\,\mathrm{cm}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(x_1=-7,5\,\mathrm{cm}\)

Odpowiedź prawidłowa

Rozwiązanie

Położenie środka ciężkości można wyznaczyć z następującej zależności:

\(\displaystyle{x_s=\frac{mx_1+3mx_2}{m+3m} }\)

\(x_1\) jest wartości ujemną wiec współrzędną \(x_2\) obliczamy jako \(x_2=10+x_1\)

\(\displaystyle{0=\frac{mx_1+3m(10+x_1)}{4m} }\)

\(4x_1=30\)

\(x_1=-7,5\,\mathrm{cm}\)

Polecenie

Wyznacz tensor momentu bezwładności. Wybierz jedną prawidłową wartość, spośród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(\hat{I}=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0,0075m & 0 \\ 0 & 0  & 0,0075m \end{bmatrix}\)

Odpowiedź prawidłowa

Wybór 2z 2

\(\hat{I}=\begin{bmatrix} 0,0075m & 3m & m \\ 0 & 0,0075m & 0 \\ 0 & 0  & 0,0075m \end{bmatrix}\)

Odpowiedź nieprawidłowa

Rozwiązanie

W ogólnym przypadku moment bezwładności układu \(N\) punktów materialnych o masach \(m_i\) i współrzędnych \((x_i,\,y_i,\,z_i)\), gdzie \(i=1,\,2,...N\) jest symetrycznym tensorem drugiego stopnia, którego składowe mają postać:

\(I_{xx}=\sum_{N}^{i=1}m_i\left ( y_i^2+z_i^2 \right )\),    \(I_{xy}=-\sum_{N}^{i=1}m_ix_iy_i\),

\(I_{yy}=\sum_{N}^{i=1}m_i\left ( x_i^2+z_i^2 \right )\),    \(I_{xz}=-\sum_{N}^{i=1}m_ix_iz_i\),

\(I_{zz}=\sum_{N}^{i=1}m_i\left ( x_i^2+y_i^2 \right )\),    \(I_{yz}=-\sum_{N}^{i=1}m_iy_iz_i\)

i można je zapisać w postaci macierzy

\(\hat{I}=\begin{bmatrix}I_{xx} &I_{xy}  &I_{xz} \\ I_{xy} &I_{yy}  &I_{yz} \\ I_{xz} &I_{yz}  &I_{zz} \end{bmatrix}\)

W naszej sytuacji wartość niezerową przyjmują składowe

\(I_{yy}=I_{zz}=m\cdot 0,075^2+3m\cdot 0,025^2\)

\(I_{yy}=I_{zz}=0,005625m+0,001875m=0,0075m\)

Odpowiedź

Tensor momentu bezwładności ma postać:

\(\hat{I}=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0,0075m & 0 \\ 0 & 0  & 0,0075m \end{bmatrix}\)