Zadanie 5.4.1.4
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.4. Zasady zachowania w ruchu obrotowym.
  4. 5.4.1 Nauka
  5. Zadanie 5.4.1.4

 Zadanie 5.4.1.4

Człowiek chodzący po tarczy
Na brzegu poziomo ustawionej tarczy o momencie bezwładności \(I\) (względem osi pionowej przechodzącej przez środek tarczy) i promieniu \(R\) znajduje się człowiek o masie \(m\). Oblicz prędkość kątową \(\omega\) tarczy, gdy człowiek zacznie się poruszać wzdłuż jej brzegu z prędkością \(v\) względem niej.

 Wskazówka teoretyczna

 Teoria - zasada zachowania momentu pędu
Zasada zachowania momentu pędu

\(\displaystyle{\sum_{i=1}^N\vec{L}_i=\sum_{j=1}^N\vec{L}_j }\)

Suma momentów pędu ciała przed zderzeniem, połączeniem lub rozpadem równa jest sumie momentów pędu ciał po zderzeniu, połączeniu lub rozpadzie.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- moment bezwładności tarczy \(I_0\),
- promień tarczy \(R\),
- masa człowieka \(m\),
- prędkość człowieka \(v\).

Szukane:
- prędkość kątowa tarczy \(\omega_t\).

Analiza sytuacji

Zadanie to można rozwiązać stosując zasadę zachowania momentu pędu układu człowiek-tarcza. Na początku człowiek i tarcza są w spoczynku, więc moment pędu układu jest równy zeru. Podczas ruchu po tarczy człowiek działa na tarczę za pośrednictwem stopy siłą \(F_t\) w kierunku przeciwnym do swojego ruch. Zgodnie z III zasadą dynamiki tarcza działa na człowieka siłą \(F_c\) taką samą co do wartości i przeciwnie skierowaną. Obie siły \(F_t\) i \(F_c\) są siłami wewnętrznymi, działającymi w układzie człowiek-tarcza.

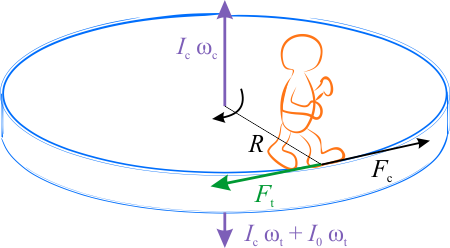
Rysunek


Jeżeli na układ nie działają żadne momenty sił, zewnętrznych to moment pędu układu pozostaje stały co do wartości, kierunku i zwrotu.

Momenty sił wewnętrznych, działające między ciałami tworzącymi układ, mogą zmienić momenty pędów poszczególnych części układu, ale suma tych zmian jest zawsze równa zero. Momenty sił wewnętrznych nie mogą zmienić momentu pędu całego układu.

Rozwiązanie

Człowiek porusza się z prędkością kątową \(\displaystyle{\omega_c=\frac{v}{R}}\) względem tarczy i jednocześnie jest unoszony przez tarczę z prędkością kątową \(\omega_t\) w kierunku przeciwnym. Zatem jego całkowity moment pędu wynosi

\(L_c=I_c\omega_t-I_c\omega_c\),

gdzie \(I_c=mR^2\) jest momentem bezwładności człowieka o masie \(m\) względem osi obrotu tarczy. Po podstawieniu otrzymujemy:

\(\displaystyle{L_c=mR^2\left (\omega_t-\frac{v}{R}\right )}\).

Moment pędu tarczy wynosi

\(L_t=I_0\omega_t\)

Z zasady zachowania momentu pędu mamy

\(L_c+L_t=0\)
 \[I_c\omega_t+I_0\omega_t=I_c\omega_c\] \[\displaystyle{mR^2\omega_t+I_0\omega_t=mR^2\frac{v}{R}}\] \[\omega_t\left (mR^2+I_0\right )=mRv\] 
\(\displaystyle{\omega_t=\frac{mRv}{mR^2+I_0} }\)

Odpowiedź

Prędkość kątowa tarczy wynosi \(\displaystyle{\omega_t=\frac{mRv}{mR^2+I_0} }\).