Zadanie 5.4.2.3
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- promień Ziemi \(R_z=6371\,\mathrm{km}\),
- przyspieszenie ziemskie \(\displaystyle{g=9,8\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- maksymalna odległość, na jaką oddali się satelita od Ziemi \(r_{max}\).
Odpowiedź
Satelita maksymalnie oddali się od Ziemi na odległość \(r_{max}\approx 1,5R_z\).
Polecenie
Wiedząc, że prędkość na niskiej orbicie to pierwsza prędkość kosmiczna, napisz zasadę zachowania momentu pędu i wyznacz z niej prędkość \(v_{m}\) satelity. Przyjmij, że promień niskiej orbity wynosi \(R_z\).
Wybierz jedną prawidłową zależność, wśród czterech przedstawionych poniżej.
\(\displaystyle{v_m=1,1\,\frac{R_z}{r_{max}}\, \sqrt{gR_z}}\)
\(\displaystyle{v_{m}=\frac{R_z}{r_{max}}v_2^2}\)
Rozwiązanie
Siła grawitacji jest siłą centralną więc moment tej siły jest równy zeru. W konsekwencji moment pędu satelity musi być zachowany. Gdy nie ma sił zewnętrznych, ze względu na potencjalność pola grawitacyjnego całkowita energia mechaniczna musi być zachowana.
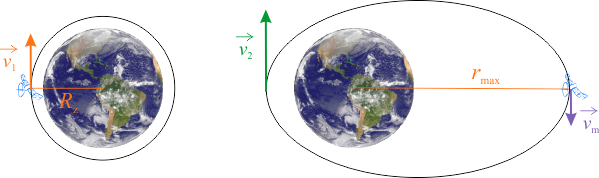
Prędkość na niskiej orbicie to pierwsza prędkość kosmiczna \(v_1=\sqrt{gR_z}\), a na podstawie danych znamy prędkość \(v_2=1,1\cdot v_1\). Teraz z zasady zachowania momentu pędu możemy napisać:
\(\displaystyle{v_m=\frac{R_z}{r_{max}}1,1\cdot v_1}\)
\(\displaystyle{v_m=1,1\,\frac{R_z}{r_{max}}\, \sqrt{gR_z}}\)
Polecenie
Zapisz zasadę zachowania energii całkowitej na jej podstawie wyznacz \(r_{max}\). Wybierz jedną prawidłową wartość, wśród dwóch przedstawionych poniżej.
\(r_{max}\approx 1,5R_z\)
Rozwiązanie
Korzystając teraz z zasady zachowania energii mechanicznej otrzymujemy
- dla punktu, w którym prędkość satelity wynosi \(v_2\):
- dla punktu, w którym prędkość satelity wynosi \(v_m\):
\(\displaystyle{E_c=\frac{mv_m^2}{2}-g\frac{R_z^2m}{r_{max}}}\)
Przyrównując obie energie i podstawiając \(v_2=1,1\cdot \sqrt{gR_z}\) oraz \(\displaystyle{v_m=1,1\,\frac{R_z}{r_{max}}\, \sqrt{gR_z}}\), otrzymujemy
\[\displaystyle{\frac{1}{2}v_2^2-gR_z=\frac{1}{2}v_m^2-g\frac{R_z^2}{r_{max}} }\] \[\displaystyle{\frac{1}{2}\cdot (1,1)^2gR_z-gR_z=\frac{1}{2}\cdot (1,1)^2\frac{R_z^2}{r_{max}^2}gR_z-g\frac{R_z^2}{r_{max}} }\] \[\displaystyle{\frac{1,21}{2}-1=\frac{1,21}{2}\frac{R_z^2}{r_{max}^2}-\frac{R_z}{r_{max}} }\] \[\displaystyle{-0,395=0,605\frac{R_z^2}{r_{max}^2}-\frac{R_z}{r_{max}} }\]
Rozwiązaniem równania kwadratowego jest para liczb \(r_1=R_z\) oraz \(r_2\approx 1,5\,R_z\). Tak więc ostatecznie mamy \(r_{max}\approx 1,5R_z\).
Odpowiedź
Satelita maksymalnie oddali się od Ziemi na odległość \(r_{max}\approx 1,5R_z\).
