Zadanie 6.1.1.3
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.1. Drgania swobodne.
  4. 6.1.1. Nauka
  5. Zadanie 6.1.1.3

 Zadanie 6.1.1.3

Amplituda drgań oscylatora
Amplituda drgań oscylatora wynosi \(6\,\mathrm{cm}\), a okres \(4\,\mathrm{s}\). Jaka jest maksymalna prędkość i przyspieszenie tego ruchu?

 Wskazówka teoretyczna

 Teoria - oscylator harmoniczny
Oscylator harmoniczny - układ drgający, poddany działaniu sił sprężystych tj. sił proporcjonalnych do przemieszczenia \(x_0\) układu od położenia równowagi:
\(F(x)=-kx_0\)

Maksymalne wartości prędkości i przyspieszenia ciała wykonującego ruch harmoniczny prosty wynoszą:

\(\displaystyle{v_{max}=x_0\omega_0 }\)

\(\displaystyle{a_{max}=x_0\omega_0^2 }\)

Użyte symbole: \(\omega_0\) - częstość kołowa, \(k\) - współczynnik proporcjonalności między siłą a wychyleniem, \(m\) - masa drgającego cała.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- amplituda drgań oscylatora \(x_0=6\,\mathrm{cm}=0,06\,\mathrm{m}\),
- okres drgań oscylatora \(T=4\,\mathrm{s}\)

Szukane:
- maksymalna prędkość ruchu \(v_{max}\),
- maksymalne przyspieszenie ruchu \(a_{max}\),

Rozwiązanie

W celu wyznaczenia maksymalnych wartości prędkości i przyspieszenia ruchu, musimy najpierw obliczyć częstość kołową drgania:

\(\displaystyle{\omega_0=\frac{2\pi}{T}=\frac{2\pi}{4} }\)

\(\displaystyle{\omega_0=\frac{\pi}{2}\,\mathrm{s^{-1}} }\)

Teraz wyznaczymy interesujące wielkości:

\(\displaystyle{v_{max}=x_0\omega_0=0,06\cdot \frac{\pi}{2}=0,03\pi \,\mathrm{\frac{m}{s}}}\)

\(\displaystyle{a_{max}=x_0\omega_0^2 =0,06\cdot \left (\frac{\pi}{2}\right )^2=0,015\pi^2\,\mathrm{\frac{m}{s^2}} }\)

Teoria - oscylator harmoniczny

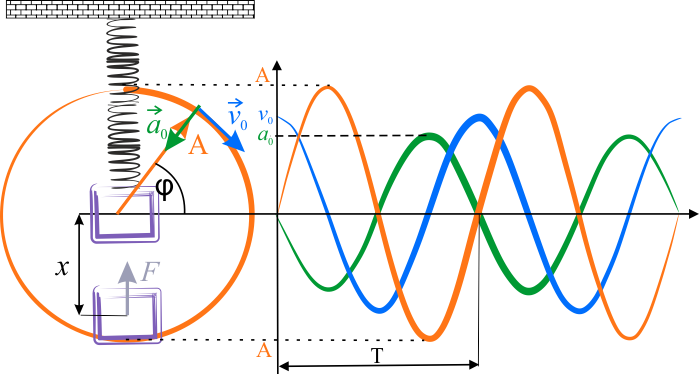
Analizę kinematyki i dynamiki oscylatora harmonicznego rozpoczniemy od przypomnienia równania

\(x(t)=x_0\cos(\sqrt{\frac{k}{m}}t+\varphi)=x_0 \cos (\omega_0 t+\varphi )\)

W powyższym wzorze \(x_0\) oznacza amplitudę drgań, \(\varphi\) jest fazą początkowa drgań, zaś \(\displaystyle{\omega_0=\sqrt{\frac{k}{m}}}\) częstością kątową (\(k\) jest współczynnikiem sprężystości, a \(m\) masą drgającego ciała). Zapisane rozwiązanie wskazuje, że oscylator harmoniczny wykonuje drgania okresowe, których okres wynosi:

\(\displaystyle{T=\frac{2\pi}{\omega_0}=2\pi\sqrt{\frac{m}{k}} }\)

Zmiany prędkości w czasie przeanalizujemy wykorzystując równanie:

\(\displaystyle{v(t)=\frac{\mathrm{d}x(t) }{\mathrm{d} t}=\frac{\mathrm{d} }{\mathrm{d} t}x_0 \cos (\omega_0 t+\varphi ) }\)

\(v_0(t)=-x_0\omega_0\sin(\omega_0 t+\varphi )\)

Prędkość ciała jest największa wtedy, gdy funkcja sinus przyjmuje wartość \(-1\). Stąd otrzymujemy

\(v_{max}=x_0\omega_0\)  lub \(\displaystyle{v_{max}=x_0\sqrt{\frac{k}{m}}}\)

Podobnie postępujemy podczas analizy dynamiki omawianego ruchu.

\(\displaystyle{a(t)=\frac{\mathrm{d^2}x(t) }{\mathrm{d} t^2}=\frac{\mathrm{d^2} }{\mathrm{d} t^2}x_0 \cos (\omega_0 t+\varphi ) }\)

\(\displaystyle{a(t)=\frac{\mathrm{d} }{\mathrm{d} t}\left ( -x_0\omega_0\sin(\omega_0 t+\varphi )\right ) }\)

\(a_0(t)=-x_0\omega_0^2\cos(\omega_0 t+\varphi )\)

Przyspieszenie ciała jest największa wtedy, gdy funkcja cosinus przyjmuje wartość \(-1\). Stąd otrzymujemy

\(a_{max}=x_0\omega_0^2\)  lub \(\displaystyle{a_{max}=x_0\frac{k}{m} }\)

Rysunek

Odpowiedź

Maksymalna prędkość i przyspieszenie tego ruchu wynoszą \(\displaystyle{v_{max}=0,03\pi \,\mathrm{\frac{m}{s}}}\) oraz

\(\displaystyle{a_{max}=0,015\pi^2\,\mathrm{\frac{m}{s^2}} }\).