Zadanie 6.1.2.5
Sprężyna
Sprężyna wydłuża się pod wpływem siły \(F_0=9,8\,\mathrm{N}\) o \(x_0=0,1\,\mathrm{m}\). Do sprężyny został podwieszony ciężarek o masie \(2\,\mathrm{kg}\) i wprawiony w drgania. Ile wynosi okres tych drgań?
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- siła działająca na sprężynę \(F_0=9,8\,\mathrm{N}\),
- wydłużenie sprężyny pod wpływem działania siły \(F_0\): \(x_0=0,1\,\mathrm{m}\),
- masa ciężarka \(m=2\,\mathrm{kg}\).
Szukane:
- okres drgań \(T\).
Odpowiedź
Okres drgań ciężarka wynosi \(0,9\,\mathrm{s}\).
Polecenie
Oblicz okres drgań sprężyny. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.
Wybór 1 z 4
\(T=0,5\,\mathrm{s}\)
\(T=0,5\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Wybór 2 z 4
\(T=0,6\,\mathrm{s}\)
\(T=0,6\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Wybór 3 z 4
\(T=0,9\,\mathrm{s}\)
Odpowiedź prawidłowa
Wybór 4 z 4
\(T=1\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Rozwiązanie
Zgodnie z prawem Hooke'a wydłużenie sprężyny jest proporcjonalne do działającej na nią siły, zgodnie ze wzorem
\(F_0=kx_0\)
gdzie \(k\) jest współczynnikiem sprężystości sprężyny.
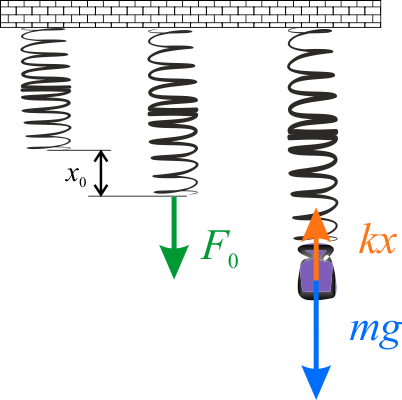
Gdybyśmy do sprężyny podwiesili jedynie ciężarek bez wprowadzenia go w drgania, to sprężyna wydłużyłaby się tak, że siła ciężkości zrównoważyłaby siłę sprężystości sprężyny. Jeżeli jednak ciężarek wprawimy w drgania (na ciężarek zadziała wtedy zmienna niezrównoważona siła \(kx\)), to okres tych drgań zależy od masy ciała i współczynnika sprężystości sprężyny, zgodnie ze wzorem
\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}}\)
Wyznaczając \(k\) z pierwszego równania mamy
\(\displaystyle{T=2\pi\sqrt{\frac{mx_0}{F_0}}}\) \(\displaystyle{\left [\mathrm{\sqrt{\frac{kg\cdot m}{N}}=\sqrt{\frac{kg\cdot m}{\frac{kg\cdot m}{s^2}}}=s } \right ]}\)
\(\displaystyle{T=2\pi\sqrt{\frac{2\cdot 0,1}{9,8}}=0,9\,\mathrm{s} }\)
Odpowiedź
Okres drgań ciężarka wynosi \(0,9\,\mathrm{s}\).
