Zadanie 6.2.1.3
Wahadło matematyczne
Małą kulkę podwieszoną do nitki o długości \(2\,\mathrm{m}\) odchylono od pionu o kąt \(3^{\circ}\), a następnie puszczono swobodnie. Kulka wykonuje drgania harmoniczne. Jaka jest prędkość kulki w najniższym punkcie toru?
Wskazówka teoretyczna
Teoria - energia potencjalna
Wzór na energię potencjalną oscylatora harmonicznego silnie zależy od warunków początkowych. Aby nie komplikować formuł rozpatrzymy warunki początkowe, przy których kąt wychylenia zależy od czasu jak
W chwili początkowej wychylenie jest maksymalne i wynosi \(\alpha_0\), więc energia potencjalna względem położenia równowagi (najniższe położenie masy wahadła matematycznego) wynosi:
Dla dowolnej chwili czasu zależność opisująca energie potencjalną przyjmuje postać
\( \alpha(t)=\alpha_0\cos(\omega_0t) \)
W chwili początkowej wychylenie jest maksymalne i wynosi \(\alpha_0\), więc energia potencjalna względem położenia równowagi (najniższe położenie masy wahadła matematycznego) wynosi:
\(E_p(t=0)=mgl(1-\cos\alpha_0) \)
Dla dowolnej chwili czasu zależność opisująca energie potencjalną przyjmuje postać
\(E_p=mgl(1-\cos\alpha(t)) \)
\(E_p=mgl\left \{1-\cos\left [ \alpha_0\cos(\omega_0t) \right ] \right \} \)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- długość nitki \(l=2\,\mathrm{m}\),
- odchylenie początkowe kulki \(\alpha=3^{\circ}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- prędkość kulki w najniższym punkcie toru \(v\).
Rozwiązanie
Mając początkowe położenie kulki (kąt odchylenia) możemy wyznaczyć energię potencjalną:
\(E_p=mgl \left ( 1-\cos 3^{\circ} \right ) \)
Z zasady zachowania energii mechanicznej możemy napisać warunek
\(E_p(\alpha=3^{\circ})=E_k(\alpha=0^{\circ})\)
\(\displaystyle{mgl \left ( 1-\cos 3^{\circ} \right )=\frac{mv_{max}^2}{2} }\)
\(\displaystyle{v_{max}=\sqrt{2gl\left ( 1-\cos 3^{\circ} \right )} }\)
\(\displaystyle{v_{max}=\sqrt{2\cdot 10\cdot 2\left ( 1-\cos 3^{\circ} \right )}\approx 0,23\,\mathrm{\frac{m}{s}} }\)
Poprawną odpowiedź możemy uzyskać również korzystając ze wzoru na maksymalną prędkość liniową kulki w tym ruchu
\(v_{max}=l\cdot \alpha_0\cdot\omega\)
\(\displaystyle{v_{max}=2\cdot \frac{3\pi}{180}\cdot\sqrt{\frac{10}{2}}\approx0,23\,\mathrm{\frac{m}{s}} }\)
Teoria - oscylator harmoniczny
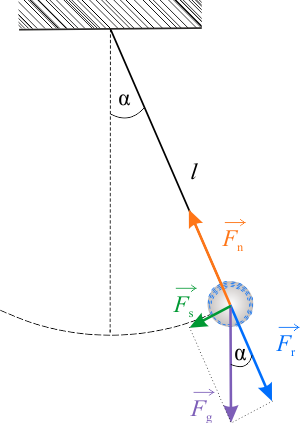
W położeniu równowagi, co na rysunku ilustruje pionowa linia przerywana, na masę \(m\) działają dwie równoważące się siły: ciężar \(F_g\) oraz naciąg nici \(F_n\). Po wychyleniu z położenia równowagi o niewielki kąt \(\alpha\), pojawia się niezerowa siła \(F_s\) styczna do toru ruchu, który jest okręgiem. Z rysunku wnioskujemy, że wartość tej siły wynosi \(F_s = F_g \sin\alpha\). Zmienia się również naciąg nieważkiej nitki od wartości \(F_n = F_g\) do wartości \(F_n = F_g \cos\alpha \) po wychyleniu o kąt \(\alpha\). Dla małych dostatecznie kątów \(\alpha\) odległość \(x\) masy \(m\) od prostej pionowej (linia przerywana) jest równa \(x=l\cdot\sin\alpha\).
Energia potencjalna wahadła
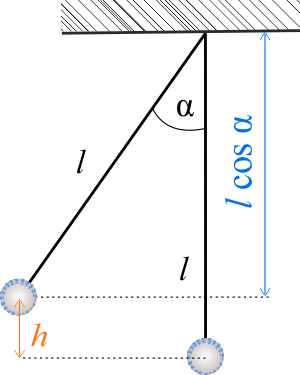
Na podstawie rysunku można wyznaczyć wysokość na jakiej znajduje się ciało
\(h(\alpha)=l-l\cos \alpha\)
Tak więc otrzymujemy
\(E_p=mgh=mgl(1-\cos\alpha(t)) \)
Odpowiedź
Szukana prędkość ma wartość \(\displaystyle{v\approx 0,23\,\mathrm{\frac{m}{s}} }\).