Zadanie 6.3.1.3
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.3. Niestandardowe problemy w ruchu drgającym.
  4. 6.3.1. Nauka
  5. Zadanie 6.3.1.3

 Zadanie 6.3.1.3

Sprężyny połączone równolegle i szeregowo
Do dwóch wiszących pionowo obok siebie identycznych sprężyn (układ równoległego połączenia) podwieszono mały ciężarek o masie \(m\) i zmierzono okres małych drgań \(T_r\) masy \(m\). Następnie sprężyny połączono ze sobą (jedną pod drugą - układ szeregowego połączenia), pozwolono im zwisać pionowo, podwieszono ten sam ciężarek, a następnie zmierzono okres \(T_{s}\) małych drgań masy \(m\). Jaki jest stosunek \(\displaystyle{ \frac{T_r}{T_s} }\)?

 Wskazówka teoretyczna

 Teoria - połączenia sprężyn
Połączenie szeregowe jest to taki rodzaj połączenia elementów , w którym koniec jednego elementu łączy się z początkiem następnego.

Połączenie równoległe jest to taki rodzaj połączenia elementów, w którym wszystkie końce oraz wszystkie początki elementów są połączone razem.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa ciężarka \(m\),
- okres małych drgań masy przy połączeniu równoległym \(T_r\),
- okres małych drgań masy przy połączeniu szeregowym \(T_s\).

Szukane:
- stosunek okresów \(\displaystyle{ \frac{T_r}{T_s} }\).

Analiza sytuacji

Rozwiązanie podzielimy na dwie część. Osobno zostanie przeanalizowana sytuacja dla połączenia szeregowego i równoległego dwóch wiszących pionowo identycznych sprężyn.

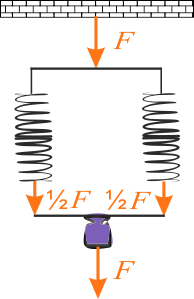
Połączenie równoległe

Po przyłożeniu do ciała zewnętrznej pionowej siły \(F\), każda ze sprężyn zostanie odkształcona (ściśnięta/rozciągnięta) o identyczną wartość odkształcenia, tj. o \(x_r\). Wypadkowa siła przyłożona do ciała jest równa

\(\displaystyle{F_r=k_rx_r=\frac{1}{2}F+\frac{1}{2}F}\)

\(F_r=k\cdot x_r+k\cdot x_r=2k\cdot x_r\)

Tak więc efektywny współczynnik sprężystości układu sprężyn połączonych równolegle wynosi

\(k_r=2k\)

Teraz możemy wyznaczyć okresy drgań

\(\displaystyle{T_r=2\pi \sqrt{\frac{m}{2k}} }\)

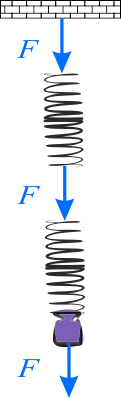
Rysunek

Połączenie szeregowe

Wypadkowe rozciągnięcie/ściśnięcie się układu sprężyn - po przyłożeniu do podwieszonego ciała - pionowej siły (działającej w górę lub w dół) \(F\) wyniesie \(x_s\), na co składają się odkształcenia obu sprężyn

\(x_s=x_1+x_2\)

przy czym, ze względu na działanie siły \(F\) na każdą ze sprężyn (siła \(F\) przyłożona do dolnej sprężyny przenoszona jest do górnej), mamy

\(\displaystyle{x_1=\frac{F}{k}}\)   \(\displaystyle{x_2=\frac{F}{k}}\)
\(\displaystyle{x_s=x_1+x_2=\frac{F}{k_s}}\)
\(\displaystyle{\frac{1}{k_s}=\frac{1}{k}+\frac{1}{k}}\)
\(\displaystyle{k_s=\frac{k}{2}}\)
Teraz możemy wyznaczyć okresy drgań

\(\displaystyle{T_s=2\pi \sqrt{\frac{2m}{k}} }\)

Rysunek
Mając wyznaczone okresy drgań masy przy dwóch różnych układach sprężyn, możemy wyznaczyć stosunek okresów \(\displaystyle{ \frac{T_r}{T_s} }\).

\(\displaystyle{T_r=2\pi \sqrt{\frac{m}{2k}} }\)  oraz  \(\displaystyle{T_s=2\pi \sqrt{\frac{2m}{k}} }\)

\(\displaystyle{\frac{T_r}{T_s}=\frac{2\pi \sqrt{\frac{m}{2k}}}{2\pi \sqrt{\frac{2m}{k}}}=\sqrt{\frac{1}{2k}\cdot \frac{k}{2}}=\frac{1}{2} }\)

Odpowiedź

Przy zmianie połączenia sprężyn od równoległego do szeregowego sprężyn okres rośnie dwukrotnie.