Zadanie 6.3.1.4
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.3. Niestandardowe problemy w ruchu drgającym.
  4. 6.3.1. Nauka
  5. Zadanie 6.3.1.4

 Zadanie 6.3.1.4

Połaczenia sprężyn
Pudełko prostopadłościenne o masie \(m\) jest połączone z dwoma sprężynami jak pokazują rysunki. Dane są stałe sprężystości \(k_1\) i \(k_2\). Wyznaczyć okresy małych drgań pudełka w obu przedstawionych przypadkach, zaniedbując siły oporów powietrza i podłoża (nie działa siła tarcia).

 Wskazówka teoretyczna

 Teoria - połączenia sprężyn
Połączenie szeregowe jest to taki rodzaj połączenia elementów , w którym koniec jednego elementu łączy się z początkiem następnego.

Połączenie równoległe jest to taki rodzaj połączenia elementów, w którym wszystkie końce oraz wszystkie początki elementów są połączone razem.
Rysunek 1
Rysunek 1 - Połączenie szeregowe
Rysunek 2
Rysunek 2 - Połączenie równoległe

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa pudełka prostopadłościennego \(m\),
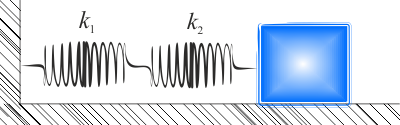
- stała sprężystości pierwszej sprężyny \(k_1\),
- stała sprężystości drugiej sprężyny \(k_2\).

Szukane:
- okresy małych drgań pudełka w połączeniu szeregowym sprężyn \(T_s\),
- okresy małych drgań pudełka w połączeniu równoległym sprężyn \(T_r\).

Analiza sytuacji

Rozwiązanie podzielimy na dwie część. Osobno zostanie przeanalizowana sytuacja dla połączenia szeregowego i równoległego dwóch wiszących pionowo identycznych sprężyn.

Rozwiązanie - połączenie szeregowe

Po przyłożeniu do ciała zewnętrznej siły \(F\) układ sprężyn z pierwszego rysunku zostanie rozciągnięty (ściśnięty) o xa, na co składają się odkształcenia (rozciągnięcie/ściśnięcie) obu sprężyn

\(x_s=x_1+x_2\)


przy czym, ze względu na działanie siły \(F\) na każdą ze sprężyn, mamy

\(\displaystyle{x_1=\frac{F}{k_1}}\)   \(\displaystyle{x_2=\frac{F}{k_2}}\)
\(\displaystyle{x_s=x_1+x_2=\frac{F}{k_s}}\)
\(\displaystyle{\frac{1}{k_s}=\frac{1}{k_1}+\frac{1}{k_2}}\)
\(\displaystyle{k_s=\frac{k_1k_2}{k_1+k_2}}\)

Teraz możemy wyznaczyć okresy drgań

\(\displaystyle{T_s=2\pi \sqrt{\frac{m}{k_s}}=2\pi \sqrt{\frac{m(k_1+k_2)}{k_1k_2}} }\)

Rozwiązanie - połączenie równoległe

Po przyłożeniu do ciała zewnętrznej siły \(F\), każda ze sprężyn zostanie odkształcona (ściśnięta/rozciągnięta) o identyczną wartość odkształcenia, tj. o \(x_r\). Wypadkowa siła przyłożona do ciała jest równa

\(\displaystyle{F_r=k_rx_r=F_1+F_2}\)

\(F_r=k_1\cdot x_r+k_2\cdot x_r=x_r(k_1+k_2)\)

Teraz możemy wyznaczyć okresy drgań

\(\displaystyle{T_r=2\pi \sqrt{\frac{m}{k_r}}=2\pi \sqrt{\frac{m}{k_1+k_2}} }\)

Odpowiedź

Okres drgań pudełka w przypadku szeregowego połączenia sprężyn wynosi \(\displaystyle{T_s=2\pi \sqrt{\frac{m(k_1+k_2)}{k_1k_2}} }\), a dla połączenia równoległego mamy \(\displaystyle{T_r=2\pi \sqrt{\frac{m}{k_1+k_2}} }\).