Rozwiązanie

W przypadku wahadła umieszczonego na wózku jadącym ruchem jednostajnie przyspieszonym w dół równi o podanym kącie nachylenia, należy zauważyć, że gdy nie ma drgań, to wahadło znajduje się w stanie równowagi, gdy nitka z ciałem jest prostopadła do nachylonej powierzchni równi. Najłatwiej jest to zrozumieć przechodząc do nieinercyjnego układu odniesienia. Wypadkowa siły ciężkości i siły bezwładności muszą dawać w wyniku wypadkową siłę skierowana prostopadle do powierzchni równi. To samo można uzasadnić z punktu widzenia spoczywającego, inercyjnego układu odniesienia. Tym razem wypadkowa siły naciągu nici oraz siły grawitacji daje siłę skierowaną równolegle do powierzchni równi. Powstałe trójkąty sił są prostokątne i naciąg nici wynosi \(F_w = mg\cos\alpha\). Wychylając wahadło z położenia równowagi, powodujemy powstanie siły ściągającej wahadło do wskazanego położenia równowagi w ruchu jednostajnie przyspieszonym. W ten sposób rolę siły ciężkości, gdy wahadło wykonuje standardowe drgania, teraz odgrywa naciąg \(F_w\).

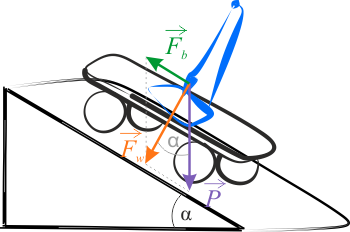
W omawianym przykładzie na wahadło będzie działać siła ciężkości \(P\) i bezwładności \(F_b\). Okres wyznaczamy z zależności\(\displaystyle{T_g=2\pi \sqrt{\frac{lm}{F_w}} }\)\(\displaystyle{T_g=2\pi \sqrt{\frac{lm}{mg\cos\alpha}}=2\pi \sqrt{\frac{l}{g\cos\alpha}} }\)