Zadanie 6.3.2.5
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.3. Niestandardowe problemy w ruchu drgającym.
  4. 6.3.2. Trening
  5. Zadanie 6.3.2.5

 Zadanie 6.3.2.5

Wahadło w przyspieszającym pojeździe
Ile wynosi okres drgań wahadła matematycznego o długości \(l\) wiszącego w pojeździe poruszającym się po poziomej powierzchni ruchem prostoliniowym jednostajnie przyspieszonym z przyspieszeniem równym \(a\)?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- długość wahadła \(l\),
- przyspieszenie pojazdu \(a\).

Szukane:
- okres drgań wahadła \(T\).

Odpowiedź

Okres drgań wahadła matematycznego wiszącego w pojeździe poruszającym się po poziomej powierzchni ruchem prostoliniowym jednostajnie przyspieszonym wynosi \(\displaystyle{T=2\pi\sqrt{ \frac{l}{\sqrt{g^2+a^2}}} }\).

Polecenie

Wyznacz okres drgań wahadła. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{T=2\pi\sqrt{ \frac{l}{\sqrt{g^2-a^2}}} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{T=2\pi\sqrt{ \frac{l}{\sqrt{g^2+a^2}}} }\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{T=2\pi\sqrt{ \frac{l}{g\sin \alpha}} }\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{T=2\pi\sqrt{ \frac{l}{g\cos\alpha}} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

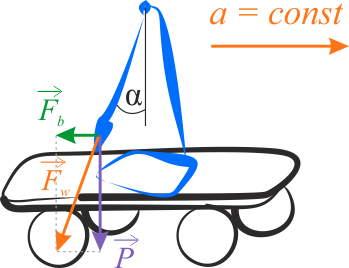
Rysunek


W omawianym przykładzie na wahadło będzie działać siła ciężkości \(P\) i bezwładności \(F_b\). Siła naciągu \(F_w\) nici w położeniu równowagi wynosi 

\(F_w=\sqrt{(mg)^2+(ma)^2} \)

Okres drgań wyznaczamy z zależności

\(\displaystyle{T=2\pi \sqrt{\frac{lm}{F_w}} }\)

\(\displaystyle{T=2\pi \sqrt{\frac{lm}{\sqrt{(mg)^2+(ma)^2}}}=2\pi \sqrt{\frac{l}{\sqrt{g^2+a^2}}} }\)

Odpowiedź

Okres drgań wahadła matematycznego wiszącego w pojeździe poruszającym się po poziomej powierzchni ruchem prostoliniowym jednostajnie przyspieszonym wynosi \(\displaystyle{T=2\pi\sqrt{ \frac{l}{\sqrt{g^2+a^2}}} }\).