Zadanie 6.3.2.6
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.3. Niestandardowe problemy w ruchu drgającym.
  4. 6.3.2. Trening
  5. Zadanie 6.3.2.6

 Zadanie 6.3.2.6

Skok na sprężystej linie
Skoczek o masie \(65\,\mathrm{kg}\) wykonuje skok bungee. Nierozciągnięta lina ma długość \(11\,\mathrm{m}\). Skoczek po oderwaniu się od pomostu spada w dół i po przebyciu \(36\,\mathrm{m}\) zaczyna być wciągany do góry. Taki skok składa się ze swobodnego spadku z wysokości \(11\,\mathrm{m}\), a następnie przez \(25\,\mathrm{m}\) skoczek jest hamowany przez rozciągająca się linę. Jeśli wartość siły z jaką lina działa na ciało jest proporcjonalna do jej wydłużenia, to ten fragment skoku można uważać za ruch harmoniczny. Jak długo trwa swobodny spadek skoczka? Wyznaczyć współczynnik sprężystości liny. Na jakiej głębokości skoku wypadkowa wszystkich sił wynosi zero?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa skoczka \(m=65\,\mathrm{kg}\),
- długość liny \(l=11\,\mathrm{m}\),
- maksymalna głębokość skoku \(H=36\,\mathrm{m}\),
- rozciągnięcie liny \(x=25\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- czas spadku swobodnego \(t\),
- współczynnik sprężystości liny \(k\),
- głębokości skoku, dla której wypadkowa wszystkich sił wynosi zero \(x_g\).

Odpowiedź

Spadek swobodny trwa \(1,48\,\mathrm{s}\), współczynnik sprężystości liny wynosi \(\displaystyle{k=74,88\,\mathrm{\frac{N}{m}}}\). Głębokość, na której wypadkowa wszystkich sił wynosi zero to \(19,68\,\mathrm{m}\).

Polecenie

Wyznacz czas spadku swobodnego skoczka. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(t=0,51\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(t=0,93\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(t=1,48\,\mathrm{s}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(t=2,03\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Ten problem jest dość złożony. Skoczek, poddany sile ciężkości, najpierw spada swobodnie przebywając odległość \(l=11\,\mathrm{m}\), kiedy to lina nie rozciąga się. Począwszy od tej głębokości na skoczka oprócz siły ciężkości zaczyna oddziaływać siła sprężystości rozciągającej się liny. Skutkiem tego ruch skoczka staje się ruchem opóźnionym niejednostajnym, aż do momentu osiągnięcia najniższego położenia, które dzieli od miejsca skoku \(36\,\mathrm{m}\). Po drodze mija miejsce, w którym wypadkowa siła jest równa zeru. Miejsce to jest położeniem \(x_r\), wokół którego odbywają się drgania i ruch skoczka. Następnie skoczek zaczyna poruszać się w górę ruchem niejednostajnie przyspieszonym, osiąga ponownie punkt \(x_r\) i kontynuuje ruch w górę. Gdy znajdzie się w odległości \(11\,\mathrm{m}\) od miejsca zeskoku, linka przestaje być naprężoną, ale skoczek – przy założeniu zachowania energii – podnosi się do miejsca, z którego rozpoczął skok bungee. Następnie opisany ruch powtarza się.

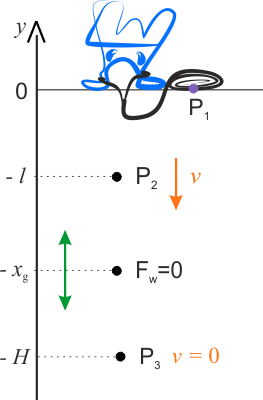
Rysunek


Policzymy czas spadku swobodnego ze wzoru \(\displaystyle{l=\frac{1}{2}gt^2 }\)

\(\displaystyle{t=\sqrt{\frac{2l}{g}} }\)

\(\displaystyle{t=\sqrt{\frac{2\cdot 11}{10}}=1,48\,\mathrm{s} }\)

Polecenie

Wyznacz współczynnik sprężystości liny. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{k=11,12\,\mathrm{\frac{N}{m}}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{k=23,21\,\mathrm{\frac{N}{m}}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{k=53,21\,\mathrm{\frac{N}{m}}}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{k=74,88\,\mathrm{\frac{N}{m}}}\)

Odpowiedź prawidłowa

Rozwiązanie

Podczas skoku skoczek spada w dół na głębokość \(H=36\,\mathrm{m}\), przy czym lina rozciąga się o \(x=25\,\mathrm{m}\). Z zasady zachowania energii możemy wyznaczyć stałą sprężystości linki

\(\displaystyle{-mgH+\frac{1}{2}kx^2=0}\)

\(\displaystyle{k=\frac{2mgH}{x^2}}\)

\(\displaystyle{k=\frac{2\cdot 65\cdot 10\cdot 36}{25^2}=74,88\,\mathrm{\frac{N}{m}}}\)

Polecenie

Oblicz na jakiej głębokości skoku wypadkowa wszystkich sił wynosi zero. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x_r=17,25\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x_r=19,68\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(x_r=21,68\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(x_r=28,25\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Obliczymy obecnie na jakiej głębokości skoku wypadkowa siła jest równa zeru. W tym celu wyznaczamy wartość rozciągnięcia \(x_r\) liny, dla której zachodzi równość

\(mg=kx_r\)

\(\displaystyle{x_r=\frac{mg}{k} }\)

\(\displaystyle{x_r=\frac{65\cdot 10}{74,88}=8,68\,\mathrm{m} }\)

Oznacza to, że na głębokości \(x_g=11+8,68 = 19,68\,\mathrm{m}\) ma miejsce zrównoważenie się wszystkich sił i jest to punkt wokół, którego odbywają się drgania skoczka.

Odpowiedź

Spadek swobodny trwa \(1,48\,\mathrm{s}\), współczynnik sprężystości liny wynosi \(\displaystyle{k=74,88\,\mathrm{\frac{N}{m}}}\). Głębokość, na której wypadkowa wszystkich sił wynosi zero to \(19,68\,\mathrm{m}\).