Zadanie 6.4.1.2
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.4. Drgania tłumione, wymuszone i złożone.
  4. 6.4.1. Nauka
  5. Zadanie 6.4.1.2

 Zadanie 6.4.1.2

Drgania wymuszone
Wartości amplitud wymuszonych drgań harmonicznych są równe dla dwóch częstości siły wymuszającej \(\displaystyle{\omega_1=400\,\mathrm{\frac{rad}{s}}}\) oraz \(\displaystyle{\omega_2=600\,\mathrm{\frac{rad}{s}}}\). Wyznacz częstość rezonansową, dla której amplituda drgań wymuszonych osiągnie maksymalną wartość.

 Wskazówka teoretyczna

 Teoria - drgania wymuszone
Drgania wymuszone – drgania odbywające się pod wpływem zewnętrznego źródła energii o zmiennym natężeniu.

Mechaniczne drgania wymuszone można przedstawić jako swobodny oscylator harmoniczny, na który działa siła \(F(t)=F_0\cos(\omega t)\). Równanie takiego ruchu można zapisać w postaci:

\(\displaystyle{\frac{\mathrm{d}^2x(t) }{\mathrm{d} t^2}+2\beta\frac{\mathrm{d}x(t) }{\mathrm{d} t}+\omega_0^2x=f_0\cos(\omega t) }\)
gdzie
\(\displaystyle{2\beta=\frac{b}{m} }\) współczynnik tłumienia; \(\displaystyle{\omega_0^2=\frac{k}{m} }\) - częstość oscylatora nietłumionego; \(\displaystyle{f_0=\frac{F_0}{m} }\);

\(\omega_r=\sqrt{\omega_0^2-2\beta^2}\) - częstość rezonansowa;
\(\displaystyle{A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} } }\) - amplituda wymuszona;

\(\displaystyle{A_r=\frac{f_0}{2\beta(\omega_0^2-\beta^2)} }\) - amplituda rezonansowa.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- pierwsza amplituda wymuszonych drgań harmonicznych \(\displaystyle{\omega_1=400\,\mathrm{\frac{rad}{s}}}\),
- druga amplituda wymuszonych drgań harmonicznych \(\displaystyle{\omega_2=600\,\mathrm{\frac{rad}{s}}}\).

Szukane:
- częstość rezonansowa, dla której amplituda \(A\) drgań wymuszonych osiągnie maksymalną wartość \(\omega_r\).

Analiza sytuacji

Amplituda wymuszona drgań harmonicznych zależy od częstości drgań siły wymuszającej według wzoru:

\(\displaystyle{A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} } }\)

gdzie \(F_0\) jest amplitudą siły wymuszającej, \(m\) - masą drgającej cząstki, \(\omega\) - częstością drgań własnych, \(\beta\) - współczynnikiem tłumienia.

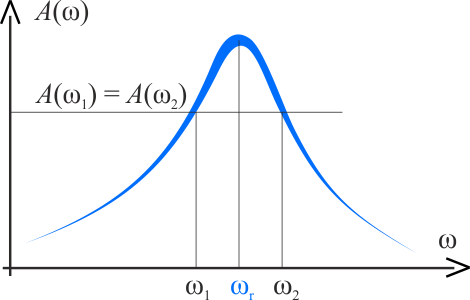
Rysunek


Jak widać na rysunku funkcja \(A(\omega)\) ma maksimum dla pewnej częstości, którą nazywamy częstością rezonansową. Zależy ona od częstości drgań własnych i współczynnika tłumienia według wzoru

\(\omega_r=\sqrt{\omega_0^2-2\beta^2}\)

Z warunku, że amplitudy są jednakowe dla częstości \(\omega_1\) i \(\omega_2\), tj. \(A(\omega_1)=A(\omega_2)\) otrzymujemy następujące równanie

\((\omega_0^2-\omega_1^2)^2+4\beta^2\omega_1^2=(\omega_0^2-\omega_2^2)^2+4\beta^2\omega_2^2\)

Rozwiązanie

W przedstawionym powyżej równaniu występują dwie niewiadome wielkości \(\omega_0\) i \(\beta\) ale po przekształceniu do postaci

\(\cancel{\omega_0^4}-2\omega_0^2\omega_1^2+\omega_1^4+4\beta^2\omega_1^2=\cancel{\omega_0^4}-2\omega_0^2\omega_2^2+\omega_2^4+4\beta^2\omega_2^2\)

\(\omega_1^4-2\omega_1^2(\omega_0^2-2\beta^2)=\omega_2^4-2\omega_2^2(\omega_0^2-2\beta^2)\)

widzimy, że wyrażenie w nawiasie jest kwadratem częstości rezonansowej

\(\omega_1^4-2\omega_1^2\omega_r^2=\omega_2^4-2\omega_2^2\omega_r^2\)

Rozwiązaniem tego równania jest częstość rezonansowa dana wzorem
  \[-2\omega_1^2\omega_r^2+2\omega_2^2\omega_r^2=\omega_2^4-\omega_1^4\] \[\omega_r^2(2\omega_2^2-2\omega_1^2)=(\omega_2^2-\omega_1^2)(\omega_2^2+\omega_1^2)\] \[\displaystyle{\omega_r=\sqrt{\frac{(\omega_2^2-\omega_1^2)(\omega_2^2+\omega_1^2)}{2(\omega_2^2-\omega_1^2)}} }\] 
\(\displaystyle{\omega_r=\sqrt{\frac{\omega_1^2+\omega_2^2}{2}} }\)

\(\displaystyle{\omega_r=\sqrt{\frac{600^2+400^2}{2}}=510\,\mathrm{\frac{rad}{s}} }\)

Odpowiedź

Częstość rezonansowa, dla której amplituda drgań wymuszonych osiągnie maksymalną wartość, wynosi \(\displaystyle{\omega_r=510\,\mathrm{\frac{rad}{s}} }\).