Zadanie 6.4.1.3
Składanie drgań
Punkt porusza się pod wpływem dwóch prostopadłych drgań składowych. Oblicz trajektorie w następujących przypadkach:
- \(x=\sin \pi t\,\mathrm{m}\) oraz \(y=0,5\cos (\pi (t+0,5))\,\mathrm{m}\),
- \(x=2\cos \omega t\,\mathrm{m}\) oraz \(y=3\sin \omega t\,\mathrm{m}\).
Wskazówka teoretyczna
Teoria - składanie drgań
Jeżeli pewien punkt jest poddany jednoczesnemu pobudzeniu przez dwa niezależne źródła drgań (sprężyny, generatory itp.), to ten punkt będzie wykonywał drganie będące sumą obu drgań. Mówimy wtedy o składaniu drgań. Chociaż składanie drgań może dotyczyć drgań o dowolnym kształcie, to ograniczymy się do sytuacji, w których oba źródła wykonują drgania harmoniczne. Możemy wyróżnić dwa interesujące przypadki szczególne:
- oba drgania odbywają się w tym samym kierunku i wtedy będziemy mieli składanie drgań równoległych. Występuje wtedy bardzo efektowne zjawisko zwane dudnieniem, które ma także ważne znaczenie w technice pomiarowej.
- oba drgania odbywają się w kierunkach prostopadłych do siebie i wtedy mówimy o składaniu drgań prostopadłych. Pod działaniem drgania wypadkowego punkt porusza się po torze, który często jest bardzo skomplikowaną krzywą mającą często fantastyczne walory graficzne. Stosunkowo najmniej skomplikowane z tych krzywych noszą nazwę krzywych Lissajous.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
1. \(x=\sin \pi t\) oraz \(y=0,5\cos (\pi(t+0,5))\)
Równanie ruchu cząstki w kierunku \(0Y\) ma fazę początkową \(0,5\pi\). W celu jej eliminacji rozpiszemy to równanie zgodnie ze wzorem na cosinus sumy dwóch kątów
\(y=\cos (\pi t+\pi\cdot 0,5)=\cos \pi t\cdot \cos 0,5\pi-\sin \pi t\cdot \sin 0,5\pi=-\sin \pi t\,\mathrm{m}\)
Ponieważ teraz oba drgania prostopadłe opisane są funkcją sinus, trajektorię toru otrzymamy najprościej dzieląc oba równania przez siebie:
\(\displaystyle{\frac{y}{x}=\frac{-0,5\sin \pi t}{\sin \pi t}=-\frac{1}{2} }\)
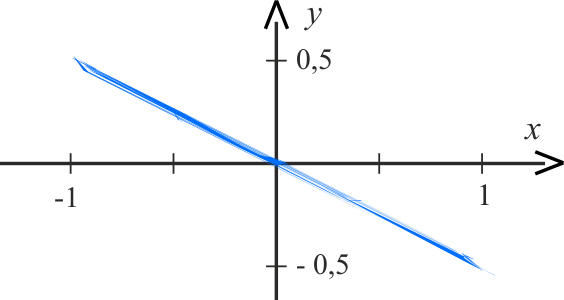
\(\displaystyle{y=-\frac{x}{2} }\)
Ze względu na funkcję sinus w równaniach ruchu mamy \(x\,\in \left \langle-1,1\right \rangle\) oraz \(y\,\in \left \langle-0,5;0,5\right \rangle\). Torem drgającego punktu jest odcinek.
2. \(x=2\cos \omega t\) oraz \(y=3\sin \omega t\)
W równaniach ruchu dzieląc wychylenia z położenia równowagi przez amplitudy tych drgań, a następnie podnosząc do kwadratu i dodając stronami, otrzymujemy
\(\displaystyle{\left (\frac{x}{2}\right )^2 +\left (\frac{y}{3}\right )^2=\cos^2(\omega t)+\sin^2(\omega t)=1}\),
czyli równanie elipsy, w której półosie mają kierunek osi układu współrzędnych.
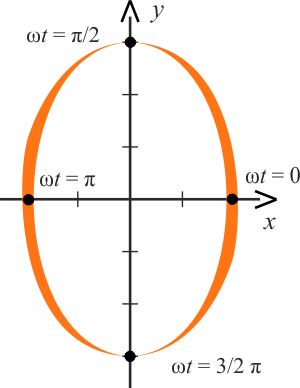
Na rysunku pokazano położenie drgającego punktu na trajektorii dla czasów, dla których odpowiednio \(\omega t=0\), \(0,5\pi\), \(\pi\), \(1,5\pi\). Stąd wynika, że ruch punktu odbywa się w kierunku przeciwnym do wskazówek zegara.
Odpowiedź
W przypadku pierwszym torem drgającego punktu jest odcinek \(AB\) gdzie \(A=(-1;0,5)\,\mathrm{m}\) oraz \(B=(1;-0,5)\,\mathrm{m}\). W przypadku drugim torem drgającego punktu jest elipsa.
