Zadanie 6.5.1.2
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.5. Rodzaje fal
  4. 6.5.1. Nauka
  5. Zadanie 6.5.1.2

 Zadanie 6.5.1.2

Poprzeczna fal stojąca
Znajdź częstotliwość drgań dla poprzecznej fali stojącej, powstałej w strunie o długości \(0,5\,\mathrm{m}\), zamocowanej w obu końcach i odpowiednio naciągniętej. Oblicz wartość naprężenia struny, jeśli masa struny przypadająca na jednostkę długości wynosi \(\displaystyle{\mu=0,01 \,\mathrm{\frac{kg}{m}} }\), a podstawowa częstotliwość drgań ma wartość \(f_1=247\,\mathrm{Hz}\).

 Wskazówka teoretyczna

 Teoria - poprzeczna fal stojąca
Fale sprężyste dzieli się na  fale podłużne i  poprzeczne. Podstawą tej klasyfikacji jest geometryczna relacja, w jakiej pozostają do siebie kierunek rozchodzenia się fali oraz kierunek drgań cząsteczek (fragmentów) ośrodka sprężystego. Jeśli więc kierunki te są prostopadłe, to mówimy, że fala jest poprzeczna.

Fala stojąca powstaje w wyniku nakładania się dwóch fal o jednakowych amplitudach i częstościach, ale rozchodzących się w dwóch przeciwnych kierunkach.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- długość struny \(L=0,5\,\mathrm{m}\),
- masa struny przypadająca na jednostkę długości \(\displaystyle{\mu=0,01 \,\mathrm{\frac{kg}{m}} }\),
- podstawowa częstotliwość drgań \(f_1=247\,\mathrm{Hz}\).

Szukane:
- częstotliwość drgań \(f_n\),
- wartość naprężenia struny \(F_0\).

Analiza sytuacji

Fala stojąca, która powstaje w strunie zamocowanej w obu końcach, w wyniku nakładania się fali biegnącej i odbitej, musi charakteryzować się tym, że na końcach struny będą węzły fali stojącej, lub inaczej mówiąc, długość jeszcze niedrgającej struny musi być równa całkowitej wielokrotności połówek długości fali.

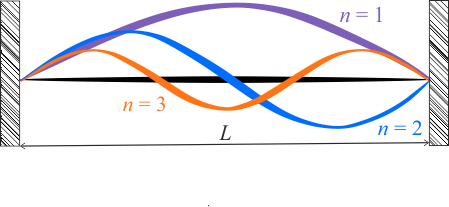
Rysunek


Możemy zapisać
\(\displaystyle{\lambda_n=2 \frac{L}{n} }\)  gdzie \(n=1,2,3,...\)

Częstotliwość drań struny wynosi

\(\displaystyle{f_n= \frac{v}{\lambda_n}=\frac{v}{2L}n }\)

gdzie \(v\) jest prędkością rozchodzenia się fali wzdłuż struny. Można pokazać, że prędkość wyraża się następującą zależnością

\(\displaystyle{v=\sqrt{\frac{F_0}{\mu}} }\)

W celu wyprowadzenia wzoru na zależność prędkości \(v\) fali od siły \(F_0\) naprężającej strunę i od masy przypadającej na jednostkę długości struny, rozpatrzmy wycinek struny o długości \(\mathrm{d}x\)

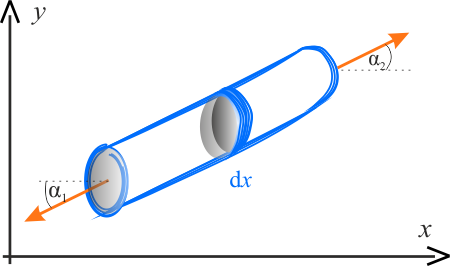
Rysunek


Końce wycinka struny tworzą z osią \(x\) małe kąty \(\alpha_1\) oraz \(\alpha_2\). Wypadkowa pionowa siła tj. siła wychylająca strunę w kierunku \(y\) wynosi

\(F_w=F\sin \alpha_2-F\sin\alpha_1\)

Dla małych kątów mamy \(\displaystyle{\alpha\approx\sin\alpha\approx \frac{\mathrm{d}y}{\mathrm{d}x} }\)

\(F_w=F \alpha_2-F\alpha_1\)

Siła wypadkowa jest równa iloczynowi masy wycinka \(\mathrm{d}m=\mu\mathrm{d}x\) i jego przyspieszenia

\(F_w=a\cdot \mathrm{d}m\)

\(\displaystyle{F_w=\mu\mathrm{d}x \frac{\partial v_y }{\partial t}=\mu\mathrm{d}x \frac{\partial^2 y }{\partial t^2} }\)

lub \(\displaystyle{\frac{\partial \alpha }{\partial x}=\frac{\mu}{F}\frac{\partial^2 y }{\partial t^2} }\)

Uwzględniając, że \(\displaystyle{\alpha=\frac{\partial y }{\partial x} }\) otrzymujemy

\(\displaystyle{\frac{\partial^2 y }{\partial x^2}=\frac{\mu}{F}\frac{\partial^2 y }{\partial t^2} }\)

Jest to równanie falowe dla struny. Podstawmy teraz do tego równania odpowiednie pochodne równania fali harmonicznej \(y=A\sin(kx-\omega t) \). Wykonujemy kolejno różniczkowanie po czasie i następnie po położeniu.

\(\displaystyle{\frac{\partial^2 y }{\partial t^2}=\frac{\partial \left [-A\omega\cos(kx-\omega t)\right ] }{\partial t} }\)
\(\displaystyle{\frac{\partial^2 y }{\partial t^2}=-A\omega^2\sin(kx-\omega t)\ }\)

\(\displaystyle{\frac{\partial^2 y }{\partial x^2}=\frac{\partial \left [Ak\cos(kx-\omega t)\right ] }{\partial t} }\)
\(\displaystyle{\frac{\partial^2 y }{\partial x^2}=-Ak^2\sin(kx-\omega t)\ }\)

Wracamy teraz do równania \(\displaystyle{\frac{\partial^2 y }{\partial x^2}=\frac{\mu}{F}\frac{\partial^2 y }{\partial t^2} }\) i po podstawieniu, mamy

\(\displaystyle{-Ak^2\sin(kx-\omega t)=-\frac{\mu}{F}A\omega^2\sin(kx-\omega t) }\)

\(\displaystyle{k^2=\frac{\mu}{F}\omega^2 }\)

\(\displaystyle{\omega^2=\frac{F}{\mu}k^2 }\)

Prędkość fali będzie więc wynosić

\(\displaystyle{v=\frac{\omega}{k}=\frac{1}{k}\sqrt{\frac{F}{\mu}}\sqrt{k^2} }\)

\(\displaystyle{v=\sqrt{\frac{F}{\mu}} }\)

Rozwiązanie

Częstotliwość drań dla ustalonej liczby \(n\) wynosi

\(\displaystyle{f_n=\frac{n}{2L}\sqrt{\frac{F_0}{\mu}} }\)

Z powyższego wzoru wyznaczamy szukane w zadaniu napięcie struny dla podstawowej częstotliwości (\(n=1\)) drgań fali stojącej.

\(F_0=4L^2\mu f_1^2\)

\(F_0=4\dot (0,5)^2\cdot 0,01 \cdot 247^2=610\,\mathrm{N}\)

\(\displaystyle{\left [\,\mathrm{m^2\cdot \frac{kg}{m}\cdot \frac{1}{s^2}=\frac{m}{s^2}\cdot kg=N }\right ]}\)

Odpowiedź

Częstotliwość drgań dla poprzecznej fali stojącej, powstałej w strunie wynosi \(\displaystyle{f_n=\frac{n}{2L}\sqrt{\frac{F_0}{\mu}} }\), natomiast wartość naprężenia struny ma wartość \(F_0=610\,\mathrm{N}\).