Zadanie 6.7.2.6
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.7. Transport energii i inne problemy
  4. 6.7.2. Trening
  5. Zadanie 6.7.2.6

 Zadanie 6.7.2.6

Kąt graniczny
Fala akustyczna pada pod kątem \(\alpha\) na powierzchnię wody. Dla jakich kątów padania fala ta nie wnika do wody? W jakiej odległości od brzegu jeziora powinien stać śpiewający człowiek, aby ryby mogły usłyszeć jego pieśń? Załóż, że człowiek jest źródłem fali monochromatycznej o prędkości fazowej fali w powietrzu \(\displaystyle{c_1=332 \,\mathrm{\frac{m}{s}}}\). Źródło dźwięku znajduje się na wysokości \(1,7\,\mathrm{m}\). Prędkość fazowa tej fali w wodzie wynosi \(\displaystyle{c_2=1500 \,\mathrm{\frac{m}{s}}}\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- Wysokość, na której znajduje się źródło dźwieku \(h=1,7\,\mathrm{m}\),
- prędkość fazowa fali w powietrzu \(\displaystyle{c_1=332 \,\mathrm{\frac{m}{s}}}\),
- prędkość fazowa fali w wodzie \(\displaystyle{c_2=1500 \,\mathrm{\frac{m}{s}}}\).

Szukane:
- kąt graniczny \(\alpha_g\),
- odległość człowieka od brzegu jeziora \(x\).

Odpowiedź

Fala nie wniknie do wody dla kątów większych od \(\alpha_g=12,79^{\circ}\). Aby emitowana przez stojącego człowieka fala wniknęła do wody, musi on stanąć bliżej niż \(40\,\mathrm{cm}\) od brzegu jeziora.

Polecenie

Oblicz kąt graniczny. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\alpha_g=6,41^{\circ}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\alpha_g=12,79^{\circ}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\alpha_g=21,3^{\circ}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\alpha_g=32,4^{\circ}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Kąt graniczny wyznaczymy z zależności

\(\displaystyle{\frac{\sin\alpha}{\sin\beta}=\frac{c_1}{c_2} }\)

\(\displaystyle{\sin\alpha_g=\frac{c_1}{c_2}\sin 90^{\circ} }\)
Rysunek

\(\displaystyle{\sin\alpha_g=\frac{332}{1500}\cdot 1=0,2213 }\)

\(\alpha_g=12,79^{\circ}\)

Polecenie

Oblicz odległość \(x\) stojącego człowieka od brzegu jeziora, przy której emitowana przez niego monochromatyczna fala akustyczna wniknie do wody. Wybierz jedną prawidłową odległość, spośród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(x <0,4\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(x <1,6\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Fala wniknie do wody, jeżeli kąt padania będzie mniejszy od kąta granicznego. Wyznaczyliśmy już kąt graniczny, który wynosi \(\alpha_g=12,79^{\circ}\). Przeprowadźmy więc obliczenia dla kąta \(\alpha=12,5^{\circ}\).

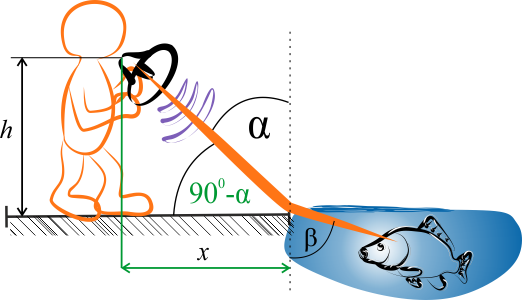
Rysunek


Z powyższego rysunku możemy zauważyć, że

\(\displaystyle{\operatorname{tg}{(90^{\circ}-\alpha)}=\frac{h}{x} }\)

Zatem odległość \(x\) wynosi

\(\displaystyle{x=\frac{h}{\operatorname{tg}{(77,5^{\circ})}}=0,38\,\mathrm{m} }\)

Odpowiedź

Fala nie wniknie do wody dla kątów większych od \(\alpha_g=12,79^{\circ}\). Aby emitowana przez stojącego człowieka fala wniknęła do wody, musi on stanąć bliżej niż \(40\,\mathrm{cm}\) od brzegu jeziora.