Zadanie 6.8.1.1
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.8. Interferencja i dyfrakcja
  4. 6.8.1. Nauka
  5. Zadanie 6.8.1.1

 Zadanie 6.8.1.1

Superpozycja dwóch fal
Dwie fale rozchodzące się wzdłuż osi \(x\) i opisane następującymi równaniami: \(u_1(x,t)=0,3\cos(4x+20t)\) w SI oraz  \(\displaystyle{u_2(x,t)=0,2\cos(4x+20t+\frac{\pi}{3}})\) w SI interferują ze sobą. Wyznacz fazę początkową i amplitudę fali wypadkowej.

 Wskazówka teoretyczna

 Teoria - zasada superpozycji fal
Jeżeli dwie fale (więcej fal) przebiegają przez ten sam obszar przestrzeni, to przemieszczenie dowolnej cząstki w ustalonej chwili czasu jest sumą przemieszczeń, które wywołałyby poszczególne fale.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- równanie pierwszej fali \(u_1(x,t)=0,3\cos(4x+20t)\) w SI,
- równanie drugiej fali \(\displaystyle{u_2(x,t)=0,2\cos(4x+20t+\frac{\pi}{3}})\) w SI.

Szukane:
- faza początkowa fali wypadkowej \(\delta\),
- amplituda fali wypadkowej \(A\).

Rozwiązanie

W myśl zasady superpozycji fala wypadkowa będzie sumą interferujących fal:

\(u(x,t)=u_1(x,t)+u_2(x,t)\)

Dla uproszczenia obliczeń zapiszemy równania fal składowych jako:

\(u_1(x,t)=0,3\cos\Phi\)  oraz  \(\displaystyle{u_2(x,t)=0,2\cos(\Phi+\frac{\pi}{3})}\)
gdzie \(\Phi=4x+20t\)

Fale składowe różnią się tylko amplitudą i fazą początkową, więc fala wypadkowa będzie miała postać:

\(\displaystyle{u(x,t)=A\cos(\Phi+\frac{\pi}{3})}\),

gdzie \(A\) jest amplitudą wypadkową.

Równanie opisujące interferencje fal, ma postać (\(\delta\) - fazą początkową):

\(\displaystyle{A\cos(\Phi+\delta)=0,3\cos\Phi+0,2\cos(\Phi+\frac{\pi}{3}) }\)
 \(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\) 
\(\displaystyle{A(\cos\Phi\cos\delta-\sin\Phi\sin\delta)=0,3\cos\Phi+0,2(\cos\Phi\cos\frac{\pi}{3}-\sin\Phi\sin\frac{\pi}{3}) }\)
\(\displaystyle{A\cos\Phi\cos\delta-A\sin\Phi\sin\delta=(0,3+0,2\cdot \cos\frac{\pi}{3})\cos\Phi-0,2\sin\Phi\sin\frac{\pi}{3} }\)
\(\displaystyle{A\cos\Phi\cos\delta-A\sin\Phi\sin\delta=0,4\cos\Phi-\frac{\sqrt{3}}{10}\sin\Phi }\)

Należy teraz porównać, znajdujące się po obu stronach znaku równości wyrażenia przy \(\cos\Phi\) oraz przy \(\sin\Phi\), gdyż powyższa równość musi być prawdziwa dla dowolnej wartości \(\Phi\). Otrzymujemy w ten sposób układ dwóch równań:

\(\begin{eqnarray} \begin{cases} A\cos\delta &=0,4\\ A\sin\delta &=\frac{\sqrt{3}}{10} \end{cases} \end{eqnarray} \)

Dzieląc powyższe równania stronami, możemy wyznaczyć fazę początkową fali wypadkowej

\(\displaystyle{\frac{A\sin\delta}{A\cos\delta}=\frac{\frac{\sqrt{3}}{10}}{0,4} }\)
\(\displaystyle{\operatorname{tg}{\delta}=\frac{\sqrt{3}}{10}\cdot \frac{10}{4}=0,43301 }\)

Faza początkowa fali wypadkowej wynosi \(\delta=23,4^{\circ}\)

Podnosząc do kwadratu równania z powyższego układu równań i dodając je stronami, otrzymujemy:

\(A^2\sin^2\delta+A^2\cos^2\delta=0,16+0,03\)
\(A^2=0,19\)
\(A=0,44\)

Równanie fali wypadkowej ma postać \(u(x,t)=0,44\cos(4x+20t+0,4086)\) w SI.

Metoda graficzna

Zadanie to można również rozwiązać metodą graficzną, wiążąc z każdą z fal wypadkowych obracający się wektor o długości równej amplitudzie fali. W naszym przypadku długości obracających się wektorów wynoszą \(A_1=0,3\) i \(A_2=0,2\). Kąt między obracającymi się wektorami jest równy różnicy faz pomiędzy interferującymi falami, czyli w tym przypadku \(\displaystyle{\frac{\pi}{3} }\)

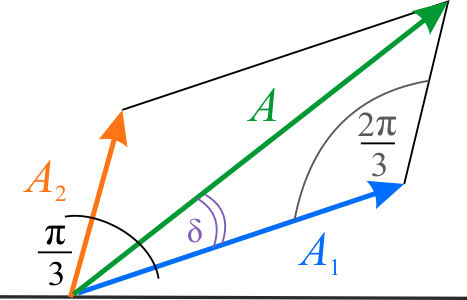
Rysunek


Amplitudę fali wypadkowej znajdziemy stosując twierdzenie cosinusów dla dowolnego z dwóch trójkątów o bokach \(A\), \(A_1\) i \(A_2\):

\(\displaystyle{A^2=A_1^2+A_2^2-2\cdot A_1\cdot A_2\cdot\cos\frac{2}{3}\pi }\)

\(\displaystyle{A^2=0,3^2+0,2^2+2\cdot 0,3\cdot 0,2\cdot\frac{1}{2} }\)

\(A^2=0,13+0,06=0,19\)
\(A=0,44\)

Kąt \(\delta\) znajdziemy stosując twierdzenie sinusów:

\(\displaystyle{\frac{0,2}{\sin\delta}=\frac{\sqrt{0,19}}{\sin\frac{2}{3}\pi} }\)

\(\displaystyle{\sin\delta=\frac{0,2\cdot\sin\frac{2}{3}\pi}{\sqrt{0,19}}=0,39736}\)

Faza początkowa fali wypadkowej wynosi \(\delta=0,4086\,\mathrm{rad}=23,4^{\circ}\)

Odpowiedź

Faza początkowa fali wypadkowej wynosi \(\delta=0,4086\,\mathrm{rad}=23,4^{\circ}\), zaś amplituda tej fali ma wartość \(A=0,44\).