Zadanie 6.8.1.2
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.8. Interferencja i dyfrakcja
  4. 6.8.1. Nauka
  5. Zadanie 6.8.1.2

 Zadanie 6.8.1.2

Interferencja
Z satelity przesłano falę nośną o częstotliwości z pasma S (\(\lambda=14\,\mathrm{cm}\)). Sygnał ten odebrał detektor promieniowania mikrofalowego, znajdujący się na brzegu jeziora na wysokości \(1\,\mathrm{m}\) nad poziomem wody. Podczas przelotu satelity detektor rejestrował kolejne maksima i minima natężenia odbieranego sygnału. Pod jakim kątem do horyzontu znajdował się satelita, w momencie zarejestrowania przez detektor trzeciego minimum natężenia?

 Wskazówka teoretyczna

 Teoria - interferencja
Interferencja fal odnosi się do fizycznych zjawisk nakładania się dwóch lub więcej ciągów falowych. W wyniku dodania się dwóch spójnych fal monochromatycznych otrzymujemy falę wypadkową o natężeniu:

\(\displaystyle{I=4I_0\cos^2\frac{\pi\Delta(nr)}{\lambda_0}=4I_0\cos^2\frac{\Delta\Phi}{2} }\)

gdzie \(\Delta\Phi\) jest różnicą faz obu fal, \(\Delta(nr)\) różnicą dróg optycznych przebytych przez nie, \(\lambda_0\) długość fali w próżni, \(n\) współczynnik załamania ośrodka.

W wyniku dodania się dwóch spójnych fal monochromatycznych, nie otrzymujemy więc po prostu fali o dwa razy większym natężeniu. Wypadkowa fal może mieć natężenie nawet czterokrotnie większe od natężenia jednej fali składowej (interferencyjne wzmocnienie) lub może zostać całkowicie wygaszona. Możliwe są również wyniki pośrednie. Zależy to od różnicy faz nakładających się fal, czyli różnicy dróg optycznych przez nie przebytych.

Powierzchnie jednakowego natężenia światła są opisane równaniem \(I=const\), czyli

\(\displaystyle{\frac{2\pi}{\lambda_0}\Delta(nr)=m\cdot 2\pi }\)

gdzie \(m\) jest rzędem interferencji. Maksima interferencyjne powstają w miejscach, gdzie rząd interferencji jest całkowity \(\displaystyle{m=0,\pm 1, \pm 2,...}\), punkty zaś, dla których rząd interferencyjny jest połówkowy \(\displaystyle{m=\pm\frac{1}{2},\pm \frac{3}{2}, \pm \frac{5}{2},...}\), tworzą minima interferencyjne.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- długość fali \(\lambda=14\,\mathrm{cm}=0,14\,\mathrm{m}\),
- wysokość, na której znajduje się detektor \(h=1\,\mathrm{m}\).

Szukane:
- kąt do horyzontu, pod jakim znajdował się satelita w momencie zarejestrowania przez detektor trzeciego minimum natężenia \(\alpha\).

Analiza sytuacji

Podczas wznoszenia się znad horyzontu źródła mikrofal, część promieniowania pada na taflę jeziora, a część pada bezpośrednio na detektor, w miejscu którego następuje interferencja. Detektor rejestruje kolejne maksima i minima, ponieważ pomiędzy drogami optycznymi tych dwóch fal nastąpiła różnica, którą należy wyznaczyć. Obydwie fale rozchodzą się w takim samym ośrodku, a ich drogi geometryczne są takie same do punktu \(A\) i \(C\) (rysunek poniżej), dlatego rozpatrywaną różnicę policzymy jako \(\Delta S=b-a\).

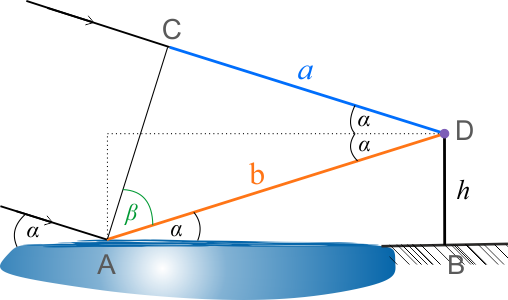
Rysunek


Punktem \(D\) oznaczono detektor. Na podstawie rysunku możemy zapisać

- z trójkąta prostokątnego \(ABD\):  \(\displaystyle{\sin\alpha=\frac{h}{b} }\)

\(\displaystyle{b=\frac{h}{\sin\alpha} }\)
- z trójkąta prostokątnego \(ADC\):  \(\displaystyle{\sin\beta=\frac{a}{b} }\)

\(\displaystyle{a=b\cdot \sin\beta=\frac{h}{\sin\alpha}\cdot \sin\beta }\)

Rozwiązanie

Różnica dróg optycznych wynosi

\(\Delta S=b-a\)
\(\displaystyle{\Delta S=\frac{h}{\sin\alpha}-\frac{h}{\sin\alpha}\cdot \sin\beta }\)

Z trójkąta prostokątnego \(ADC\) wiemy, że \(\beta=90^{\circ}-2\alpha\)

\(\displaystyle{\Delta S=\frac{h}{\sin\alpha}-\frac{h}{\sin\alpha}\cdot \sin(90^{\circ}-2\alpha) }\)

\(\displaystyle{\Delta S=\frac{h}{\sin\alpha}-\frac{h}{\sin\alpha}\cdot \cos(2\alpha) }\)

\(\displaystyle{\Delta S=\frac{h}{\sin\alpha}(1-\cos(2\alpha)) }\)   \(\cos 2\alpha=1-2\sin^2\alpha\) 

\(\displaystyle{\Delta S=\frac{h}{\sin\alpha}\cdot 2\sin^2(\alpha)=2h\sin\alpha }\)

Fala odbita od powierzchni wody zmienia fazę o \(\pi\).  Fala odbijając się od ośrodka optycznie gęstszego (o większym współczynniku załamania \(n\)) zmienia swoją fazę o \(\pi\). Natomiast, gdy odbicie zachodzi od powierzchni ośrodka rzadszego optycznie, fala odbija się bez zmiany fazy.  Uwzględniając tę zmianę, otrzymujemy warunek opisujący różnicę faz pomiędzy dwoma falami, które interferują na detektorze:

\(\displaystyle{\Delta\Phi=\pi+k\cdot \Delta S=\pi+\frac{2\pi}{\lambda}\cdot 2h\sin\alpha }\)

Ekstrema interferencyjne zaobserwujemy dla \(\Delta\Phi=m\cdot 2\pi\), a ponieważ interesuje nas trzecie minimum (\(\displaystyle{m=\frac{5}{2}}\)), mamy:

\(\displaystyle{\pi+\frac{2\pi}{\lambda}\cdot 2h\sin\alpha=\frac{5}{2}\cdot 2\pi }\)

\(\displaystyle{1+\frac{4h}{\lambda}\cdot \sin\alpha=5}\)

\(\displaystyle{\sin\alpha=\frac{\lambda}{h}=\frac{0,14}{1} }\)

Kąt, dla którego \(\sin\alpha=0,14\) to \(\alpha=8^{\circ}\).

Odpowiedź

Kąt do horyzontu, pod jakim znajdował się satelita w momencie zarejestrowania przez detektor trzeciego minimum natężenia, ma miarę \(\alpha=8^{\circ}\).