Zadanie 6.8.1.3
Siatka dyfrakcyjna
Ile prążków interferencyjnych zobaczymy, gdy oświetlimy siatkę dyfrakcyjną o odległości między szczelinami \(2\,\mathrm{\mu m}\) laserem o długości fali \(650\,\mathrm{nm}\)? Ile prążków będzie widzianych w przypadku, gdy zmienimy siatkę dyfrakcyjną o dwa razy większej ilości rys na minimetr?
Wskazówka teoretyczna
Teoria - siatka dyfrakcyjna
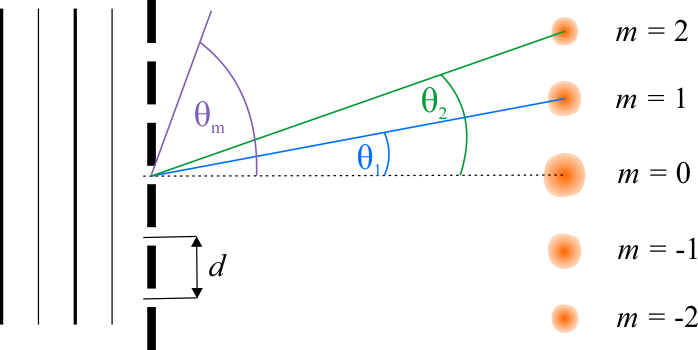
Siatka dyfrakcyjna składa się z układu równoległych i jednakowo rozmieszczonych wielu szczelin. Po przejściu przez siatkę dyfrakcyjną monochromatycznej fali płaskiej, na ekranie zobaczymy układ maksimów i minimów natężenia światła. Położenie m-tego jasnego prążka opisane jest zależnością:
gdzie \(d\) oznacza stałą siatki (odległość między najbliższymi szczelinami), \(m\) jest liczbą całkowitą i oznacza rząd widma, \(\theta_m\) kąt pod jakim powstaje m-ty prążek interferencyjny, \(\lambda\) długość fali światła padającego na siatkę dyfrakcyjną.
\(d\sin\theta_m=m\lambda\)
gdzie \(d\) oznacza stałą siatki (odległość między najbliższymi szczelinami), \(m\) jest liczbą całkowitą i oznacza rząd widma, \(\theta_m\) kąt pod jakim powstaje m-ty prążek interferencyjny, \(\lambda\) długość fali światła padającego na siatkę dyfrakcyjną.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- długość fali \(\lambda=650\,\mathrm{nm}\),
- stała pierwszej siatki dyfrakcyjnej \(d_1=2\,\mathrm{\mu m}\),
- stała drugiej siatki dyfrakcyjnej \(d_2=1\,\mathrm{\mu m}\).
Szukane:
- ilość widzianych prążków.
Analiza sytuacji
Maksima interferencyjne, obserwowane przy pomocy siatki dyfrakcyjnej, można wyznaczyć z zależności
\(d\sin\theta_m=m\lambda\)
Występowanie maksymalnej ilości prążków, które mogą być obserwowane na ekranie za siatką, związane jest z tym, że kąt ugięcia światła na szczelinach może maksymalnie przyjąć wartość \(90^{\circ}\). W rozwiązaniu należy obliczyć rząd widma dla kąta \(\theta_m=90^{\circ}\).
Rozwiązanie
Rząd widma wyznaczamy z zależności
\(\displaystyle{m=\frac{d\sin\theta_m}{\lambda} }\)
Dla pierwszej siatki mamy
\(\displaystyle{m_1=\frac{d_1\sin 90^{\circ}}{\lambda} }\)
\(\displaystyle{m_1=\frac{2\cdot 10^{-6}\cdot 1}{650\cdot 10^{-9}}\approx 3,07 }\)
Rząd widma może przyjąć tylko wartości całkowite, co w naszym przypadku daje wynik \(m_1=3\). Oznacza to, że widzimy prążek zerowy (w centralnej części widma) oraz kolejne maksima dla \(m=1\), \(m=2\) oraz \(m=3\). Nie możemy również zapomnieć o maksimach z drugiej strony prążka zerowego, czyli kolejno rzędy \(m=-1\), \(m=-2\) oraz \(m=-3\). W sumie mamy \(7\) prążków.
Druga siatka jest dwa razy gęstsza od pierwszej, czyli odległości między szczelinami są dwa razy mniejsze. Stała siatki wynosi więc \(d_2=d_1\cdot 0,5=1\cdot 10^{-6}\,\mathrm{m}\). W tym przypadku mamy
\(\displaystyle{m_2=\frac{1\cdot 10^{-6}\cdot 1}{650\cdot 10^{-9}}\approx 1,5 }\)
Po zmianie siatki, obserwujemy prążki dla rzędów \(m=0\), \(m=1\) oraz \(m=-1\), co nam daje trzy maksima. Zamiana siatki na gęstszą powoduje wzrost odległości między kolejnymi maksimami interferencyjnymi "rozrzedzenie widma", co z kolei zmniejsza ilość widzianych prążków. Tym razem mamy \(3\) prążki.
Odpowiedź
W przypadku pierwszej siatki dyfrakcyjnej zobaczymy \(7\) maksimów interferencyjnych. Zmiana siatki na dwa razy gęstszą, spowoduje zmniejszenie ilości prążków do \(3\).
