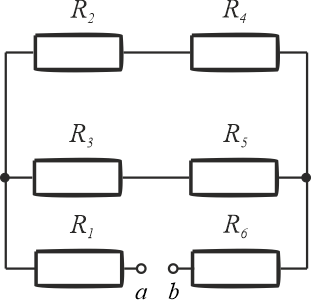
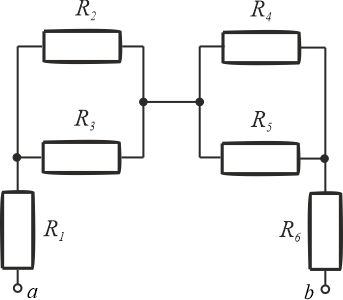
Zadanie 7.1.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- wartości rezystancji: \(R_2=R_5=500\,\mathrm{\Omega}\), \(R_3=R_4=100\,\mathrm{\Omega}\), \(R_1=\frac{25}{3}\,\mathrm{\Omega}\) oraz \(R_6=25\,\mathrm{\Omega}\).
Szukane:
- rezystancja zastępcza układu \(R_z\).
Odpowiedź
Rezystancja zastępcza wynosi: \(R_Z=200\,\mathrm{\Omega}\).
Polecenie
Zastanów się w jaki sposób można jeszcze przedstawić schemat połączeń tych rezystorów. Wybierz jeden prawidłowy układ spośród dwóch.
Rozwiązanie
Przedstawiony schemat oporników można przekształcić, czyli narysować schemat w inny sposób. Podczas przekształcenia należy zwrócić uwagę na węzły. W pierwszym kroku można zmienić położenie rezystorów \(R_1\) i \(R_6\), tak aby zaciski \(ab\) były na zewnątrz.
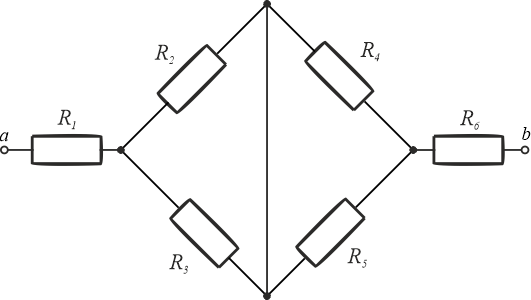
Następnie zmieniamy kąt nachlanie pozostałych czterech rezystorów.
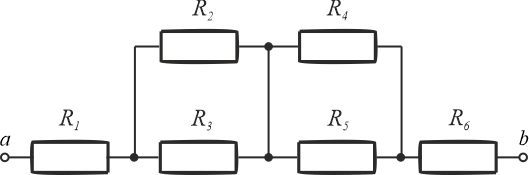
Pomiędzy rezystorami \(R_2\) a \(R_4\) oraz \(R_3\) a \(R_5\) są węzły. Fakt ten wskazuje, że oporniki \(R_2\) i \(R_3\) oraz \(R_4\) i \(R_5\) połączone są równolegle. Oba węzły można zastąpić jednym, ponieważ między nimi nie ma rezystora. W ten sposób otrzymujemy schemat widoczny w polu "Wybór 2 z 2".
Polecenie
Oblicz rezystancję zastępczą od strony zacisków \(a\) i \(b\). Wybierz jedną prawidłową wartość spośród czterech.
Rozwiązanie
Oporniki \(R_2\) i \(R_3\) oraz \(R_4\) i \(R_5\) połączone są równolegle. Oba te zestawy można zstąpić pojedynczymi rezystorami \(R_{23}\) oraz \(R_{45}\):
\(\displaystyle{R_{23}=\frac{R_2\cdot R_3}{R_2+R_3} }\) oraz \(\displaystyle{R_{45}=\frac{R_4\cdot R_5}{R_4+R_5} }\)
\(\displaystyle{R_{23}=\frac{500\cdot 100}{500+100}=\frac{250}{3}\,\mathrm{\Omega} }\) oraz \(\displaystyle{R_{45}=\frac{100\cdot 500}{100+500}=\frac{250}{3}\,\mathrm{\Omega} }\)
Teraz mamy cztery rezystory połączone szeregowo: \(R_1\), \(R_{23}\), \(R_{45}\) oraz \(R_6\). Rezystancję zastępczą obliczymy sumując wartości tych rezystorów.
\(R_Z=R_1+R_{23}+R_{45}+R_6\)
\(\displaystyle{R_Z=\frac{25}{3}+\frac{250}{3}+\frac{250}{3}+\frac{75}{3}=\frac{600}{3} }\)
\(R_Z=200\,\mathrm{\Omega}\)
Odpowiedź
Rezystancja zastępcza wynosi: \(R_Z=200\,\mathrm{\Omega}\).