Zadanie 7.1.2.3
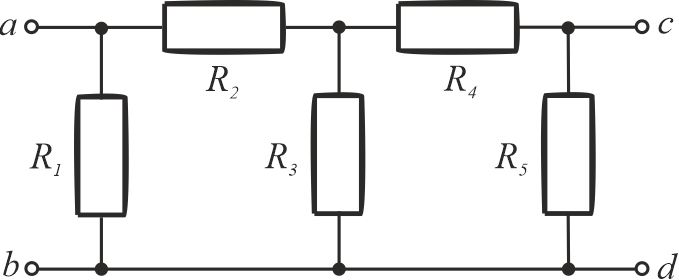
Wartości rezystorów: \(R_1=R_3=300\,\mathrm{\Omega}\), \(R_2=50\,\mathrm{\Omega}\), \(R_4=100\,\mathrm{\Omega}\) oraz \(R_5=200\,\mathrm{\Omega}\).
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- Wartości rezystorów: \(R_1=R_3=300\,\mathrm{\Omega}\), \(R_2=50\,\mathrm{\Omega}\), \(R_4=100\,\mathrm{\Omega}\) oraz \(R_5=200\,\mathrm{\Omega}\).
Szukane:
- rezystancja zastępcza układu od strony zacisków \(ab\): \(R_{ab}\),
- rezystancja zastępcza układu od strony zacisków \(cd\): \(R_{cd}\).
W przypadku takich samych rezystancji:
- rezystancja zastępcza układu od strony zacisków \(ab\): \(R2_{ab}\),
- rezystancja zastępcza układu od strony zacisków \(cd\): \(R2_{cd}\).
Odpowiedź
Rezystancje zastępcze wynoszą odpowiednio \(R_{ab}=120\,\mathrm{\Omega}\) oraz \(R_{cd}=113\,\mathrm{\Omega}\). Dla takich samych rezystancji mamy: \(\displaystyle{R2_{ab}=R2_{cd}=\frac{5}{8}R }\).
Polecenie
Oblicz rezystancję zastępczą od strony zacisków \(ab\). Wybierz jedną prawidłową wartość spośród czterech.
\(R_{ab}=50\,\mathrm{\Omega}\)
\(R_{ab}=60\,\mathrm{\Omega}\)
Rozwiązanie
Rezystory \(R_4\) oraz \(R_5\) połączone są szeregowo, więc
\[R_{45}=R_4+R_5=100+200=300\,\mathrm{\Omega}\]
Rezystory \(R_3\) oraz \(R_{45}\) połączone są równolegle i mają takie same wartości, stąd
\[\displaystyle{R_{345}=\frac{R_3}{2}=\frac{300}{2}=150\,\mathrm{\Omega} }\]
Rezystory \(R_2\) oraz \(R_{345}\) połączone są szeregowo, więc
\[R_{2-5}=R_2+R_{345}=50+150=200\,\mathrm{\Omega}\]
Rezystory \(R_1\) oraz \(R_{2-5}\) połączone są równolegle:
\[\displaystyle{R_{ab}=\frac{R_1\cdot R_{2-5}}{R_1+R_{2-5}} }\]
\[\displaystyle{R_{ab}=\frac{300\cdot 200}{300+200}=120\,\mathrm{\Omega} }\]
Polecenie
Oblicz rezystancję zastępczą od strony zacisków \(cd\). Wybierz jedną prawidłową wartość spośród czterech.
Rozwiązanie
Rezystory \(R_1\) oraz \(R_2\) połączone są szeregowo, więc
\[R_{12}=R_1+R_2=300+50=350\,\mathrm{\Omega}\]
Rezystory \(R_3\) oraz \(R_{12}\) połączone są równolegle, stąd
\[\displaystyle{R_{123}=\frac{R_3\cdot R_{12}}{R_3+R_{12}} }\]
\[\displaystyle{R_{123}=\frac{300\cdot 350}{300+350}=161,539\,\mathrm{\Omega} }\]
Rezystory \(R_4\) oraz \(R_{123}\) połączone są szeregowo, więc
\[R_{1-4}=R_4+R_{123}=100+161,539=261,539\,\mathrm{\Omega}\]
Rezystory \(R_5\) oraz \(R_{1-4}\) połączone są równolegle:
\[\displaystyle{R_{cd}=\frac{R_5\cdot R_{1-4}}{R_5+R_{1-4}} }\]
\[\displaystyle{R_{cd}=\frac{200\cdot 261,539}{200+261,539}=113,333\,\mathrm{\Omega} }\]
Polecenie
Oblicz rezystancję zastępczą od strony zacisków \(ab\) oraz \(cd\), w przypadku gdy wszystkie rezystory mają tą samą wartość. Wybierz jedną prawidłową wartość spośród trzech.
\(\displaystyle{R2_{cd}=\frac{5}{8}R}\)
\(\displaystyle{R2_{cd}=\frac{3}{8}R}\)
\(\displaystyle{R2_{cd}=\frac{5}{3}R}\)
Rozwiązanie
Rezystory \(R_1\) oraz \(R_2\) połączone są szeregowo, więc
\[R_{12}=R+R=2R\]
Rezystory \(R_3\) oraz \(R_{12}\) połączone są równolegle, stąd
\[\displaystyle{R_{123}=\frac{R_3\cdot R_{12}}{R_3+R_{12}} }\]
\[\displaystyle{R_{123}=\frac{R\cdot 2R}{R+2R}=\frac{2}{3}R }\]
Rezystory \(R_4\) oraz \(R_{123}\) połączone są szeregowo, więc
\[R_{1-4}=R_4+R_{123}=R+\frac{2}{3}R=\frac{5}{3}R\]
Rezystory \(R_5\) oraz \(R_{1-4}\) połączone są równolegle:
\[\displaystyle{R_{cd}=\frac{R_5\cdot R_{1-4}}{R_5+R_{1-4}} }\]
\[\displaystyle{R_{cd}=\frac{R\cdot \frac{5}{3}R}{R+\frac{5}{3}R}=\frac{5}{8}R }\]
Odpowiedź
Rezystancje zastępcze wynoszą odpowiednio \(R_{ab}=120\,\mathrm{\Omega}\) oraz \(R_{cd}=113\,\mathrm{\Omega}\). Dla takich samych rezystancji mamy: \(\displaystyle{R2_{ab}=R2_{cd}=\frac{5}{8}R }\).
