Zadanie 6.8.2.2
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.8. Interferencja i dyfrakcja
  4. 6.8.2. Trening
  5. Zadanie 6.8.2.2

 Zadanie 6.8.2.2

Prązki Newtona
Za pomocą soczewki płaskorównoległej i płaskiej płytki obserwujemy pierścienie Newtona w świetle lasera HeNe \(\lambda=632,8\,\mathrm{nm}\). Odległość między pierwszym a drugim jasnym pierścieniem wynosi \(0,451\,\mathrm{mm}\). Jaki jest promień krzywizny soczewki?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Teoria - prążki Newtona

Teoria - prążki Newtona

Obraz interferencyjny w postaci pierścieni Newtona otrzymuje się przy użyciu warstwy powietrza o zmiennej grubości, powstającej między soczewką wypukłą o dużym promieniu krzywizny, a płytką płaskorównoległą.

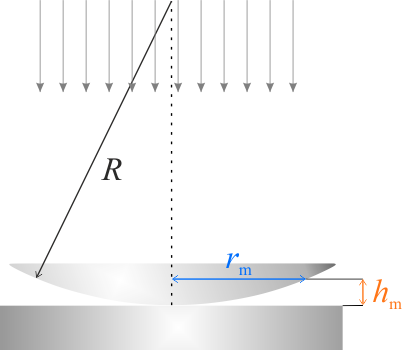
Rysunek


Promienie światła padające pionowo na płaską powierzchnię soczewki, ulegają odbiciu kolejno od płaskiej powierzchni soczewki, od jej zakszywionej powierzchni oraz od górnej powierzchni płytki płaskorównoległej. Te ostatnie interferują z promieniami odbitymi od zakrzywionej powierzchni soczewki, dając obraz składający się z jasnych i ciemnych współśrodkowych pierścieni.

Jasne pierścienie w obrazie interferencyjnym są efektem złożenia fal świetlnych, dla których różnica faz \(\Delta\Phi\) jest równa wielokrotności \(2\pi\). Rożnica ta wynika z przebycia przez promień odbity od górnej powierzchni płaskiej płytki drogi dłuższej o \(2h_m\) oraz ze zmiany fazy przy jego odbiciu o \(\pi\) (zmiana fazy przy odbiciu od ośrodka optycznie gęstszego), czyli warunek powstania jasnych pierścieni jest następujący:

\(\displaystyle{\Delta\Phi=\frac{2\pi}{\lambda}\cdot 2h_m+\pi=m\cdot 2\pi }\),   gdzie \(m=1, 2, 3,...\)

Wynika stąd, że

\(\displaystyle{h_m=(2m-1)\cdot\frac{\lambda}{4} }\)

Dane i szukane

Dane:
- długość fali \(\lambda=632,8\,\mathrm{nm}=632,8\cdot 10^{-9}\,\mathrm{m}\),
- odległość między pierwszym a drugim jasnym pierścieniem \(r_2-r_1=0,451\,\mathrm{mm}=4,51\cdot 10^{-4}\,\mathrm{m}\).

Szukane:
- promień krzywizny soczewki \(R\).

Odpowiedź

Promień krzywizny soczewki wynosi \(1,2\,\mathrm{m}\).

Polecenie

Wyznacz promień krzywizny soczewki. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(R=12\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(R=6\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(R=1,2\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(R=0,6\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Warunek powstania jasnych pierścieni jest następujący (wyjaśnienie znajduje się w teorii zamieszczonej pod treścią zadania):

\(\displaystyle{\Delta\Phi=\frac{2\pi}{\lambda}\cdot 2h_m+\pi=m\cdot 2\pi }\),   gdzie \(m=1, 2, 3,...\)

Wynika stąd, że

\(\displaystyle{h_m=(2m-1)\cdot\frac{\lambda}{4} }\)

Rysunek


 Z rysunku można również odczytać, że (tw. Pitagorasa):

\(r_m^2=R^2-(R-h_m)^2=2Rh_m-h_m^2\approx 2Rh_m\)

Zastosowane przybliżenie wynika z tego, że pierścienie Newtona obserwuje się przy warunku \(h_m<Podstawiając do ostatniego równania wyrażenie na \(h_m\), mamy wzór określający promień \(m\)-tego jasnego pierścienia Newtona:

\(\displaystyle{r_m^2=2R\cdot (2m-1)\cdot\frac{\lambda}{4}  }\)

\(\displaystyle{r_m=\sqrt{\frac{R\lambda}{2}\cdot (2m-1)} }\)

Odległość między pierwszym a drugim jasnym pierścieniem jest więc równa

\(\displaystyle{r_2-r_1=\sqrt{\frac{R\lambda}{2}\cdot (4-1)}-\sqrt{\frac{R\lambda}{2}\cdot (2-1)} }\)

Po   \[\displaystyle{r_2-r_1=\sqrt{\frac{R\lambda}{2}}\left ( \sqrt{3}-\sqrt{1}\right ) }\] \[\displaystyle{(r_2-r_1)^2=\frac{R\lambda}{2}\left ( \sqrt{3}-1\right )^2 }\] \[\displaystyle{R=\frac{2(r_2-r_1)^2}{\lambda 2 (2-\sqrt{3})} }\]  mamy

\(\displaystyle{R=\frac{(r_2-r_1)^2}{\lambda (2-\sqrt{3})} }\)

\(\displaystyle{R=\frac{(0,451\cdot 10^{-3})^2}{632,8\cdot 10^{-9}\cdot (2-\sqrt{3})}=1,199 }\)

\(R=1,2\,\mathrm{m}\)

Odpowiedź

Promień krzywizny soczewki wynosi \(1,2\,\mathrm{m}\).