Zadanie 6.8.2.4
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.8. Interferencja i dyfrakcja
  4. 6.8.2. Trening
  5. Zadanie 6.8.2.4

 Zadanie 6.8.2.4

Siatka dyfrakcyjna
Na siatkę dyfrakcyjną o \(1000\) rysach na \(\mathrm{mm}\) pada fala płaska o długości \(440\,\mathrm{nm}\). Oblicz odległość między pierwszym a drugim maksimum widma obserwowanego na ekranie oddalonym od siatki o \(0,6\,\mathrm{m}\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- ilość rys na milimetr \(N=1000\),
- długość fali \(\lambda=440\,\mathrm{nm}\),
- odległość ekranu od siatki \(x=0,6\,\mathrm{m}\).

Szukane:
- odległość między pierwszym a drugim maksimum widma obserwowanego na ekranie \(y\).

Odpowiedź

Odległość między pierwszym a drugim maksimum widma obserwowanego na ekranie wynosi \(82\,\mathrm{cm}\).

Polecenie

Oblicz kąty pod jakim ugięte są fale tworzące maksimum pierwszego i drugiego rzędu. Wybierz jedną prawidłową odpowiedź, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(\alpha_1=26,1^{\circ}\)

\(\alpha_2=61,6^{\circ}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\alpha_1=42,6^{\circ}\)

\(\alpha_2=77,1^{\circ}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Stała siatki wynosi

\(\displaystyle{d=\frac{1\,\mathrm{mm}}{1000}=\frac{0,001}{1000}=1\,\mathrm{\mu m} }\)

Kąt ugięcia promieni wyznaczymy z zależności

\(\displaystyle{\sin\alpha=\frac{m\lambda}{d} }\)

\(\displaystyle{\sin\alpha_1=\frac{1\cdot 440\cdot 10^{-9} }{1\cdot 10^{-6}}=0,44 }\)

\(\alpha_1=0,455599\,\mathrm{rad}=26,1^{\circ}\)

\(\displaystyle{\sin\alpha_2=\frac{2\cdot 440\cdot 10^{-9} }{1\cdot 10^{-6}}=0,88 }\)

\(\alpha_2=1,075862\,\mathrm{rad}=61,6^{\circ}\)

Polecenie

Oblicz odległość między pierwszym a drugim maksimum widma obserwowanego na ekranie. Wybierz jedną prawidłową odpowiedź, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(y=0,31\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 2

\(y=0,82\,\mathrm{m}\)

Odpowiedź prawidłowa

Rozwiązanie

Znając odległość ekranu od siatki oraz kąt ugięcia możemy obliczyć odległość pierwszego i drugiego maksimum od prążka rzędu zerowego.

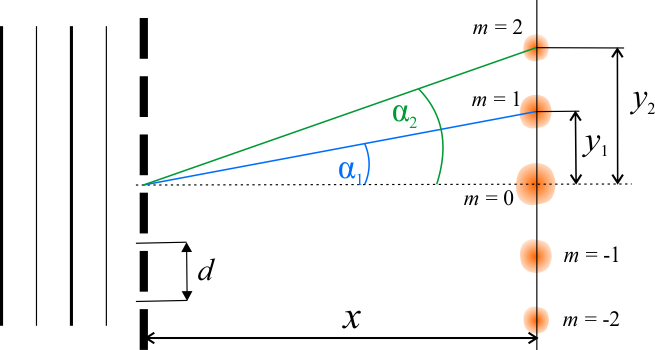
Rysunek

\(y_1=x\cdot \operatorname{tg}{\alpha_1}\)
\(y_1=0,6\cdot 0,49=0,29\)
\(y_1=0,29\,\mathrm{m}\)

\(y_2=x\cdot \operatorname{tg}{\alpha_2}\)
\(y_2=0,6\cdot 1,8527=1,11\)
\(y_2=1,11\,\mathrm{m}\)

Odległość między tymi maksimami wynosi

\(y=y_2-y_1=1,11-0,29=0,82\)
\(y=0,82\,\mathrm{m}\)

Odpowiedź

Odległość między pierwszym a drugim maksimum widma obserwowanego na ekranie wynosi \(82\,\mathrm{cm}\).