1.  W pierwszym kroku wyznaczamy dziedzinę funkcji \({\displaystyle f(x)=\frac{\sqrt{x}}{x^{2}+4}}.\)
Musimy założyć, że \(x\geq 0 \ \wedge \ x^{2}+4\neq 0.\) Ponieważ \( x^{2}+4\neq 0\) dla każdego \(x\) rzeczywistego, zatem pozostaje założenie \(x\geq 0.\) Aby funkcja \(f\) była różniczkowalna na dziedzinie musimy wykluczyć jeszcze \(x=0,\) gdyż w tym punkcie nie istnieje pochodna naszej funkcji.
Zatem dziedziną jest zbiór liczb dodatnich \(D_{f}=\mathbb{R}_{+}.\)

2. W kolejnym etapie, wyznaczamy własności funkcji i punkty przecięcia się wykresu funkcji \(f\) z osiami układu współrzędnych.

1. Dziedzina funkcji.
\[ \begin{array}{l}
{\displaystyle f(x)=\frac{3x+2}{x-1}}\\
x-1\neq 0\\
x\neq 1
\end{array}\]
Zatem
\[D=\mathbb{R}\setminus \left \{ 1 \right \}.\]
2. Punkty przecięcia się wykresu funkcji z osiami układu współrzędnych.
\[ \begin{array}{l}
x=0 \ \ \Rightarrow  \ \ {\displaystyle f(0)=\frac{0+2}{0-1}=-2}\\
f(x)=0 \ \ \Rightarrow \ \ {\displaystyle \frac{3x+2}{x-1}=0} \ \ \Rightarrow \ \ 3x+2=0 \ \ \Rightarrow  \ \ {\displaystyle x=-\frac{2}{3}}
\end{array}\]
Zatem:

• \(\left (0,-2  \right )\) - punkt przecięcia z osią  \(OY.\)
• \({\displaystyle \left ( -\frac{2}{3},0 \right )}\) - punkt przecięcia z osią \(OX\) - miejsce zerowe.

3. Granice funkcji. Asymptoty.
\[ \begin{array}{l}
{\displaystyle \lim_{x \to \pm \infty}\frac{3x+2}{x-1}=\lim_{x \to \pm\infty}\frac{3+\frac{2}{x}}{1-\frac{1}{x}}=
\lim_{x \to \pm \infty}\frac{3+\cancelto{0}{\frac{2}{x}}}{1-\cancelto{0}{\frac{1}{x}}}=3}\\
\end{array}\]
\[ \begin{array}{l}
{\displaystyle \lim_{x \to 1^{+}}\frac{3x+2}{x-1}=\left [ \frac{+}{+} \right ]=\infty}\\
{\displaystyle \lim_{x \to 1^{-}}\frac{3x+2}{x-1}=\left [ \frac{+}{-} \right ]=-\infty}
\end{array}\]
\[ \begin{array}{l}
{\displaystyle A=\lim_{x \to \pm \infty}\frac{\frac{3x+2}{x-1}}{x}=\lim_{x \to \pm \infty}\frac{\frac{3}{x}+\frac{2}{x^{2}}}{1-\frac{1}{x}}=\lim_{x \to \pm \infty}\frac{\cancelto{0}{\frac{3}{x}}+\cancelto{0}{\frac{2}{x^{2}}}}{1-\cancelto{0}{\frac{1}{x}}}=\frac{0}{1}=0}\\
{\displaystyle B=\lim_{x \to \pm \infty}\frac{3x+2}{x-1}=3}\\
y=0x+3\\
y=3
\end{array}\]
Zatem prosta \(y=3\) jest asymptotą poziomą obustronną.

4. Pochodna funkcji. Monotoniczność i ekstrema.
\[ \begin{array}{l}
{\displaystyle f(x)=\frac{3x+2}{x-1}}\\
{\displaystyle f'(x)=\frac{3\cdot (x-1)-(3x+2)\cdot 1}{\left (x-1  \right )^{2}}=\frac{3x-3-3x-2}{\left (x-1  \right )^{2}}=\frac{-5}{\left (x-1  \right )^{2}}\lt 0}
\end{array}\]
Zatem na obu przedziałach \(\left ( -\infty;1 \right )\) oraz \(\left ( 1;\infty \right )\) funkcja jest malejąca. Nie posiada ekstremum.

5. Druga pochodna funkcji. Wklęsłość, wypukłość i punkty przegięcia.
\[ \begin{array}{l}
{\displaystyle f''(x)=-5 \cdot \left (-\frac{1}{\left (x-1  \right )^{4}}\cdot 2(x-1)  \right )=\frac{10(x-1)}{(x-1)^{4}}}\\
10(x-1)=0\\
x=1
\end{array}\]
Ponieważ \(x=1\) nie należy do dziedziny funkcji \(f,\) zatem nie jest to punkt przegięcia. W jedynce natomiast druga pochodna funkcji zmienia znak z ujemnego na dodatni.
Zatem:

• w przedziale \(\left ( -\infty;1 \right )\) funkcja jest wklęsła,
• w przedziale \(\left ( 1;\infty \right )\) funkcja jest wypukła.

\[ \begin{array}{l}
f(x)=x\textrm{ arctg } x\\
1. \ \  D=\mathbb{R}\\
2. \ \ f(-x)=-x\cdot \textrm{ arctg}(-x)=-x \cdot (-\textrm{ arctg} x)=x\textrm{ arctg} x=f(x) - \textrm{ funkcja parzysta }
\\
3. \ \  x=0 \ \ \Rightarrow \ \ f(0)=0\cdot \textrm{ arctg } 0=0\\
f(x)=0 \ \ \Rightarrow \ \ x\textrm{ arctg } x=0 \ \ \Rightarrow \ \ x=0 \ \ \vee \ \  \textrm{ arctg } x=0 \ \ \Leftrightarrow \ \ x=0\\
(0,0) - \textrm{ punkt przecięcia z osiami układu współrzędnych}\\
\\
{\displaystyle 4. \ \ \lim_{x \to \infty}x\textrm{ arctg } x=\left [ \infty \cdot \frac{\pi}{2} \right ]=\infty}
\\
{\displaystyle \lim_{x \to -\infty}x\textrm{ arctg } x=\left [ -\infty \cdot \left (-\frac{\pi}{2}  \right ) \right ]=\infty}
\\
{\displaystyle A= \lim_{x \to \infty}\frac{f(x)}{x}=\lim_{x \to \infty} \textrm{ arctg } x=\frac{\pi}{2}}\\
{\displaystyle B=\lim_{x \to \infty}\left [ f(x)- \frac{\pi}{2} x\right ]=\lim_{x \to \infty}\left [ x\textrm{ arctg } x - \frac{\pi}{2} x\right ]=\lim_{x \to \infty}\left [ x\left (\textrm{ arctg } x - \frac{\pi}{2}   \right )\right ]=\left [ \infty \cdot 0 \right ]= \lim_{x \to \infty} \frac{\textrm{ arctg } x - \frac{\pi}{2} }{\frac{1}{x}}=\left [ \frac{0}{0} \right ] \stackrel{H}=}\\
{\displaystyle =\lim_{x \to \infty} \frac{ \frac{1}{1+x^{2}} }{-\frac{1}{x^{2}}}=\lim_{x \to \infty}\frac{-x^{2}}{1+x^{2}}=\lim_{x \to \infty}\frac{-1}{\frac{1}{x^{2}}+1}=\lim_{x \to \infty}\frac{-1}{\cancelto{0}{\frac{1}{x^{2}}}+1}=-1}\\
{\displaystyle y=\frac{\pi}{2}x-1 - \textrm{asymptota ukośna prawostronna}}\\
\\
{\displaystyle A= \lim_{x \to -\infty}\frac{f(x)}{x}=\lim_{x \to -\infty} \textrm{ arctg } x=-\frac{\pi}{2}}\\
{\displaystyle B=\lim_{x \to -\infty}\left [ f(x)+ \frac{\pi}{2} x\right ]=\lim_{x \to -\infty}\left [ x\textrm{ arctg } x + \frac{\pi}{2} x\right ]=\lim_{x \to -\infty}\left [ x\left (\textrm{ arctg } x + \frac{\pi}{2}   \right )\right ]=\left [ -\infty \cdot 0 \right ]= \lim_{x \to -\infty} \frac{\textrm{ arctg } x + \frac{\pi}{2} }{\frac{1}{x}}=\left [ \frac{0}{0} \right ] \stackrel{H}=}\\
{\displaystyle =\lim_{x \to -\infty} \frac{ \frac{1}{1+x^{2}} }{-\frac{1}{x^{2}}}=\lim_{x \to -\infty}\frac{-x^{2}}{1+x^{2}}=\lim_{x \to -\infty}\frac{-1}{\frac{1}{x^{2}}+1}=\lim_{x \to -\infty}\frac{-1}{\cancelto{0}{\frac{1}{x^{2}}}+1}=-1}\\
{\displaystyle y=-\frac{\pi}{2}x-1 - \textrm{asymptota ukośna lewostronna}}\\
{\displaystyle 5. \ \ f'(x)=1\cdot \textrm { arctg }x+x\cdot \frac{1}{1+x^{2}}=\textrm { arctg }x+\frac{x}{1+x^{2}}}\\
\\
{\displaystyle \textrm { arctg }x+\frac{x}{1+x^{2}}=0 }\\
{\displaystyle \textrm { arctg }x=-\frac{x}{1+x^{2}}  \ \ \Leftrightarrow \ \ x=0 \ - \textrm{ minimum funkcji }f}
\end{array}\]

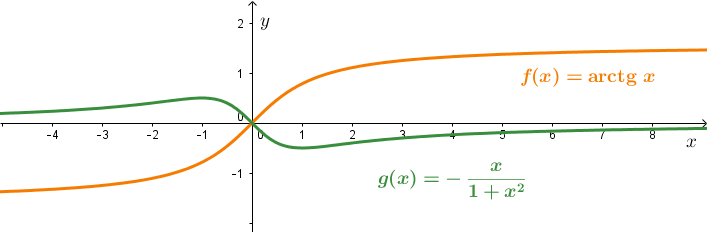
\[ \begin{array}{l}
{\displaystyle \textrm { arctg }x \gt -\frac{x}{1+x^{2}} \ \ \Leftrightarrow \ \ x \in \left ( 0; \infty \right ) \ - \textrm{ funkcja rosnąca }}\\
{\displaystyle \textrm { arctg }x\lt -\frac{x}{1+x^{2}}\ \ \Leftrightarrow \ \ x \in \left ( -\infty;0 \right ) \ - \textrm{ funkcja malejąca }}\\
\\
{\displaystyle 6. \ \ f''(x)=\frac{1}{1+x^{2}}+\frac{1(1+x^{2})-x\cdot 2x}{(1+x^{2})^{2}}=\frac{1}{1+x^{2}}+\frac{1+x^{2}-2x^{2}}{(1+x^{2})^{2}}=\frac{1+x^{2}+1-x^{2}}{(1+x^{2})^{2}}=\frac{2}{(1+x^{2})^{2}} \gt 0 \ - \textrm{ funkcja wypukła na całej dziedzinie}}
\end{array}\]