Poniżej znajduje się 7 zadań, w których dokładnie jedna odpowiedź jest prawidłowa. Wybierz właściwą odpowiedź i sprawdź jej poprawność przyciskiem "Sprawdź" lub na końcu "Sprawdź poprawność odpowiedzi".
Zadanie 1
Obszar między krzywymi \({\displaystyle y=(x-2)^{2}-2, \ \ y=x-4}\) zaznaczony jest na rysunku:
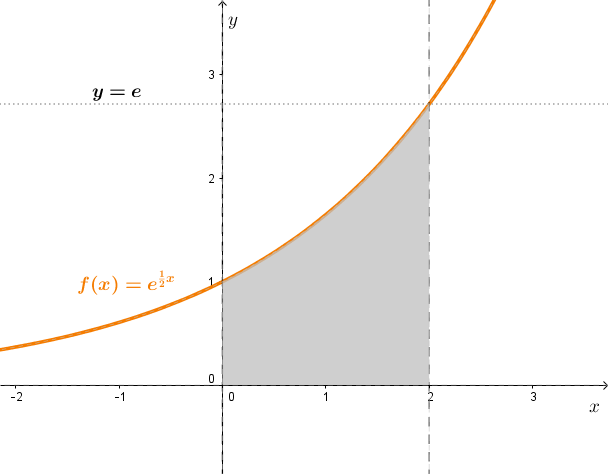
Zadanie 2
Wybierz funkcje, których wykresy ograniczają obszar przedstawiony na rysunku.
Podsumowanie

