Zadanie 9.1
  1. Analiza matematyczna 1
  2. 9. Całka oznaczona
  3. Zadanie 9.1

 Polecenie

Korzystając z definicji całki oznaczonej oblicz podaną całkę.

 Wskazówki

Definicja całki oznaczonej

Jeżeli dla każdego  Podziałem odcinka \(\left \langle a;b \right \rangle\) na \(n\) części (podprzedziałów), gdzie \(n\in \mathbb{N}\), nazywamy każdy zbiór punktów \(P_{n} = \left \{ x_{0}, x_{1}, x_{2} , ..., x_{n} \right \} \) spełniających warunek \(a = x_{0} < x_{1} < x_{2} < ... < x_{n} = b.\)   Ciąg podziałów \(\left (P_{n} \right )\) nazywamy normalnym, jeżeli \({\displaystyle \lim_{n \to \infty} \delta _{n}=0}.\)
Średnicą podziału \(P_{n}\) nazywamy liczbę \(\delta _{n}={\displaystyle \max_{1\leqslant k\leqslant n}\Delta x_{k}}\) tj. długość najdłuższego z podprzedziałów \(\left \langle x_{k-1}, x_{k} \right \rangle.\)   przedziału \(\left \langle a;b \right \rangle\) i dowolnego wyboru argumentów \(\xi_{k} \), ciąg sum częściowych  Sumę \({\displaystyle S\left ( P_{n} \right )=\sum_{k=1}^{n}f(\xi _{k})\Delta _{x_{k}}}\) nazywamy sumą całkową funkcji f na przedziale \(\left \langle a;b \right \rangle\).   ma tę samą granicę skończoną, to granicę tę nazywamy całką oznaczoną Riemanna funkcji \(f\) na przedziale \(\left \langle a;b \right \rangle\) i oznaczamy symbolem \({\displaystyle \int_{a}^{b}f(x)\ dx}.\)
Zatem \[{\displaystyle \int_{a}^{b}f(x)\ dx=\lim_{n \to \infty}\sum_{k=1}^{n}f(\xi _{k})\Delta _{x_{k}}}.\]

O funkcji \(f\) mówimy, że jest całkowalna w sensie Riemanna na przedziale \(\left \langle a;b \right \rangle\) (lub krócej całkowalna, gdy z kontekstu wynika o jaką całkę chodzi).

Liczbę \(a\) nazywamy dolną, natomiast \(b\) - górną granicą całkowania.

Interpretacja geometryczna sumy całkowej
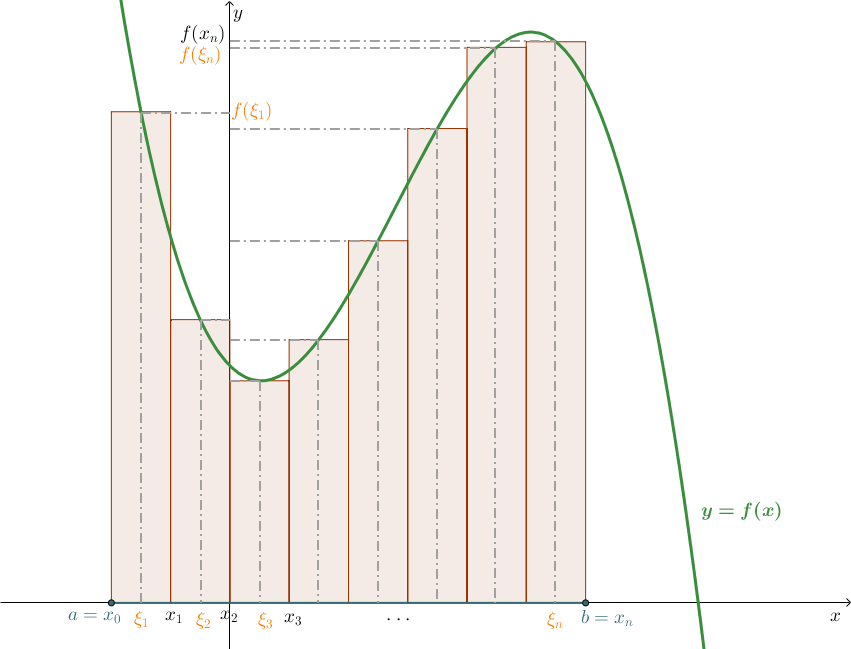
_rysunek_9.1.3
Zgodnie z przytoczonym wzorem każdy składnik sumy całkowej możemy interpretować jako pole prostokąta o podstawie \(\Delta x_{k}\) i wysokości \(f(\xi _{k}) \), zaś suma całkowa jest sumą pól takich prostokątów.
Interpretacja geometryczna całki oznaczonej
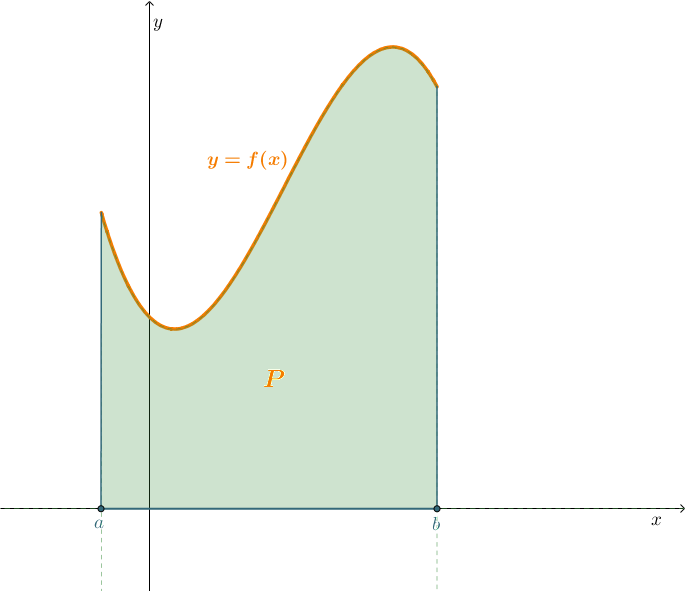
_rysunek_9.1.4
Niech \(y=f(x)\) będzie funkcją ciągłą, nieujemną na przedziale \(\left \langle a;b \right \rangle\). Z interpretacji geometrycznej sum całkowych wynika, że całka oznaczona, jako granica ciągu tych sum, określa pole figury płaskiej w układzie prostokątnym kartezjańskim, ograniczonej wykresem funkcji \(f\), osią \(Ox\) oraz prostymi \(x = a\) i \(x = b\), nazywanej trapezem krzywoliniowym.
Zatem \({\displaystyle |P|=\int_{a}^{b}f(x)\ dx}.\)

Gdy funkcja \(f\) jest niedodatnia na przedziale \(\left \langle a;b \right \rangle\) (jej wykres leży pod osią \(Ox\)), wówczas całka oznaczona podaje pole trapezu krzywoliniowego ze znakiem minus  \({\displaystyle |P|=-\int_{a}^{b}f(x)\ dx}.\)
Uwaga 1
Dla funkcji \(f\) całkowalnej na \(\left \langle a;b \right \rangle\) oraz \(a\lt  b\) zachodzi:
\[\int_{a}^{b}f(x)\ dx=-\int_{b}^{a}f(x)\ dx.\]
Uwaga 2
Dla funkcji całkowalnej \(f\)
\[\int_{a}^{a}f(x)\ dx=0.\]

Twierdzenia

Twierdzenie (o całkowalności funkcji ciągłej)
Każda funkcja ciągła na \(\left \langle a;b \right \rangle\) jest całkowalna na tym przedziale w sensie Riemanna.
Fakt (obliczanie całek przy pomocy sumy całkowej podziału równomiernego
Jeżeli funkcja \(f\) jest całkowalna na przedziale \(\left \langle a;b \right \rangle,\) to 
\[\int_{a}^{b}f(x)\ dx=\lim_{n \to \infty}\left [ \frac{b-a}{n}\sum_{k=1}^{n}f\left ( a+k\frac{b-a}{n} \right ) \right ].\]
Uwaga. Istnienie powyższej granicy nie zapewnia całkowalności funkcji, przykładem jest funkcja Dirichleta.

Własności całki oznaczonej

Własność 1
Dla każdej funkcji ciągłej \(f\) na odcinku \(\left \langle a;b \right \rangle\) i dowolnego \( c \in \left \langle a;b \right \rangle\) zachodzi:
\[\int_{a}^{b}f(x)\ dx=\int_{a}^{c}f(x)\ dx+\int_{c}^{b}f(x)\ dx.\]
Własność 2
Dla funkcji \(f\) ciągłej na odcinku \(\left \langle a;b \right \rangle\) takiej, że \(A\leqslant f(x)\leqslant B\) zachodzi:
\[A(b-a)\leqslant \int_{a}^{b}f(x)\ dx\leqslant B(b-a).\]
Własność 3
Niech funkcja \(f\) będzie całkowalna na odcinku \(\left \langle a;b \right \rangle,\) wówczas:
\[\int_{a}^{b}\alpha f(x)\ dx=\alpha \int_{a}^{b}f(x)\ dx.\]
Własność 4
Niech funkcje \(f\) i \(g\) będą całkowalne na odcinku \(\left \langle a;b \right \rangle,\) wówczas:
\[\int_{a}^{b}\left [f(x)+g(x)  \right ]\ dx= \int_{a}^{b}f(x)\ dx+\int_{a}^{b}g(x)\ dx.\]
Własność 5
Niech funkcje \(f\) i \(g\) będą całkowalne na odcinku \(\left \langle a;b \right \rangle,\) wówczas iloczyn \(f(x)\cdot g(x)\) jest również funkcją całkowalną.

Uwaga !!!

Nie jest prawdziwy wzór: \({\displaystyle \int_{a}^{b}\left [f(x)\cdot g(x) \right ]\ dx= \int_{a}^{b}f(x)\ dx\cdot \int_{a}^{b}g(x)\ dx}.\)
Własność 6
Niech funkcja \(f\) będzie całkowalna na odcinku \(\left \langle a;b \right \rangle,\) wówczas \(\left | f(x) \right |\) jest również całkowalna na \(\left \langle a;b \right \rangle\) oraz zachodzi wzór
\[\left | \int_{a}^{b}f(x)\ dx \right |\leqslant  \int_{a}^{b}\left |f(x)  \right |\ dx.\]
Własność 7
Niech funkcja \(f\) będzie całkowalna na odcinku \(\left \langle a;b \right \rangle\) oraz \(f(x)\geqslant 0,\) wówczas:
\[\int_{a}^{b}f(x)\ dx\geqslant 0.\]
Własność 8
Niech funkcje \(f\) i \(g\) będą całkowalne na odcinku \(\left \langle a;b \right \rangle\) oraz \(f(x)\leqslant g(x),\) wówczas:
\[\int_{a}^{b}f(x)\ dx\leqslant \int_{a}^{b}g(x)\ dx.\]
\({\displaystyle \int_{1}^{5}x\ dx}\)

 Rozwiązanie

Obliczmy całkę oznaczoną \({\displaystyle \int_{1}^{5}x\ dx}\), korzystając z jej definicji.

Funkcja podcałkowa \(f(x)=x\) jest ciągła, zatem na mocy twierdzenia o całkowalności funkcji ciągłej, całka ta istnieje. Przy dowolnym wyborze ciągu podziałów normalnych odcinka \(\left \langle 1;5  \right \rangle\) oraz układu punktów pośrednich ciąg \(n\) - tych sum całkowych Riemanna \((Sn)_{n=1}^{\infty}\) jest zawsze zbieżny do tej samej granicy. Wybieramy jeden szczególny ciąg podziałów normalnych \((\Delta_{n})_{n=1}^{\infty}\) odcinka \(\left \langle 1;5  \right \rangle\) oraz układy punktów pośrednich tak, by łatwo obliczyć granicę  \(
{\displaystyle \lim_{n \to \infty}S_{n}}.\) Dla ustalonego \(n\) punktami podziału \({\displaystyle x_{k}=1+\frac{4}{n}k,\ \ (k=0,…,n)}\) oraz punkty pośrednie \(\xi_{k}=x_{k},\ \ (k=1,…,n).\) Każdy z odcinków \(\left \langle x_{k-1};x_{k} \right \rangle\) ma tę samą długość \({\displaystyle \Delta_{x_{k}}=\frac{4}{n}}.\)
Czyli \[\delta _{n}=\max \left \{ \Delta _{x_{k}}:k=1,2,\cdots,n  \right \}=\frac{4}{n}\] oraz \[\lim_{n\to \infty}\delta _{n}=0.\]
Możemy teraz obliczyć całkę, korzystając z  \({\displaystyle \int_{a}^{b}f(x)\ dx=\lim_{n \to \infty}\left [ \frac{b-a}{n}\sum_{k=1}^{n}f\left ( a+k\frac{b-a}{n} \right ) \right ]}\) .
\[ \begin{array}{l}
{\displaystyle \int_{1}^{5}x\ dx=\lim_{n\to \infty}\left [\frac{4}{n}\sum_{k=1}^{n}\left ( 1+ k\frac{4}{n}\right ) \right ]=
\lim_{n\to \infty}\left [\frac{4}{n}\sum_{k=1}^{n}1+ \frac{16}{n^{2}}\sum_{k=1}^{n} k \right ]=
\lim_{n\to \infty}\left [\frac{4}{n}\cdot n+ \frac{16}{n^{2}}(1+2+\cdot +n)  \right ]=
\lim_{n\to \infty}\left [\frac{4}{n}\cdot n+ \frac{16}{n^{2}}\frac{1+n}{2}\cdot n \right ]=
\lim_{n\to \infty}\left [4+8\frac{1+n}{n}\right ]=4+8\lim_{n\to \infty}\frac{1+n}{n}=
4+8\lim_{n\to \infty}\frac{\cancelto{0}{\frac{1}{n}}+1}{1}=4+8=12.}
\end{array}\]

 Odpowiedź

\({\displaystyle \int_{1}^{5}x\ dx=12}\)

 Polecenie

Korzystając z definicji całki oznaczonej oblicz całkę \({\displaystyle \int_{0}^{1}e^{x}\ dx}\).

 Odpowiedź

\({\displaystyle \int_{0}^{1}e^{x}\ dx=e-1}\)

 Rozwiązanie

Ponieważ funkcja \(f(x)=e^{x}\) jest całkowalna na przedziale \(\left \langle 0;1 \right \rangle,\) zatem możemy skorzystać ze  \({\displaystyle \int_{a}^{b}f(x)\ dx=\lim_{n \to \infty}\left [ \frac{b-a}{n}\sum_{k=1}^{n}f\left ( a+k\frac{b-a}{n} \right ) \right ]}\) .
\[ \begin{array}{l}
{\displaystyle \int_{0}^{1}e^{x}\ dx=\lim_{n\to \infty}\left [ \frac{1-0}{n}\sum_{k=1}^{n}e^{0+k\frac{1-0}{n}} \right ]=\lim_{n\to \infty} \frac{1}{n}\sum_{k=1}^{n}e^{\frac{k}{n}}=\lim_{n\to \infty} \frac{1}{n}\left (e^{\frac{1}{n}} +e^{\frac{2}{n}}+\cdot +e^{\frac{n}{n}} \right )=\lim_{n\to \infty} \frac{1}{n}\frac{e^{\frac{1}{n}}\cdot \left ((e^{\frac{1}{n}})^{n}-1  \right )}{e^{\frac{1}{n}}-1}=\lim_{n\to \infty} \frac{e^{\frac{1}{n}}\cdot \left (e-1  \right )}{\frac{e^{\frac{1}{n}}-1}{\frac{1}{n}}}=\lim_{n\to \infty} \frac{e^{\cancelto{0}{\frac{1}{n}}}\cdot \left (e-1  \right )}{\cancelto{1}{\frac{e^{\frac{1}{n}}-1}{\frac{1}{n}}}}=1(e-1)=e-1.}
\end{array}\]
W obliczeniach stosujemy wzór na sumę \(n\) - wyrazów ciągu geometrycznego oraz na granicę \({\displaystyle \lim_{x \to 0}\frac{e^{x}-1}{x}=1}.\)