Szkicujemy okręgi \(x^{2}+y^{2}=1\) oraz  \((x-1)^{2}+(y-1)^{2}=1\) w układzie współrzędnych.

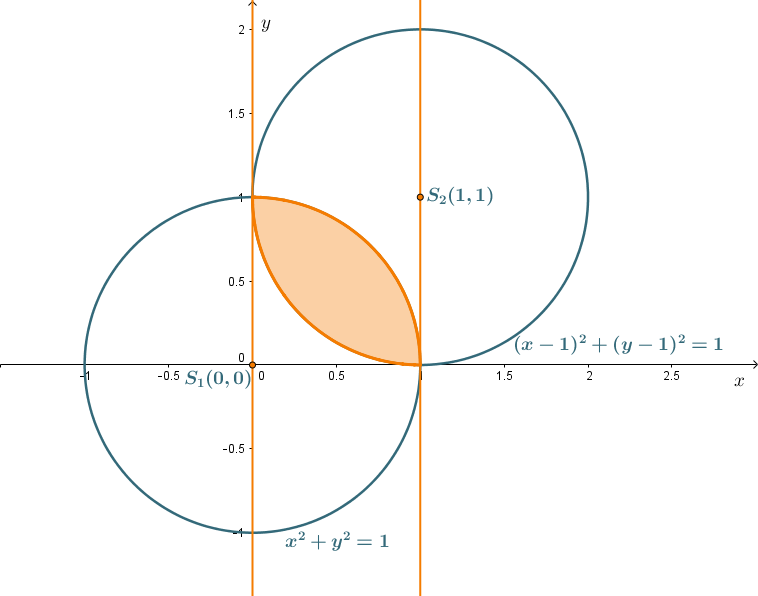
Pole zacieniowanego obszaru to całka oznaczona w granicach całkowania od \(0\) do \(1\) z różnicy funkcji opisującej krzywą \(x^{2}+y^{2}=1\) w pierwszej ćwiartce układu współrzędnych oraz krzywą \((x-1)^{2}+(y-1)^{2}=1\) (dolna część) .
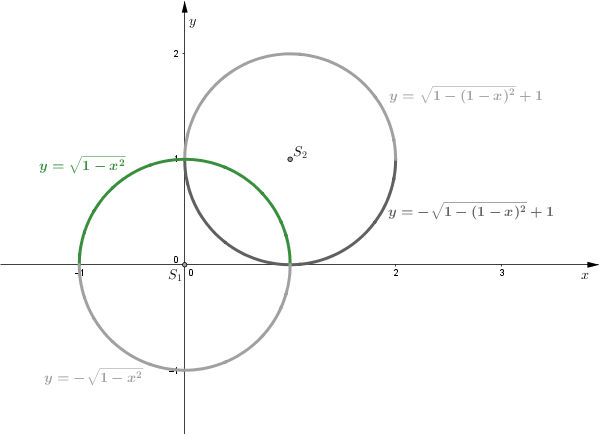
Wyznaczamy z równań okręgów \(y.\)
\(x^{2}+y^{2}=1\\
y^{2}=1-x^{2}\\
y=\pm \sqrt{1-x^{2}}\)
Wybieramy dodatni znak, gdyż interesuje nas część okręgu znajdująca się nad osią \(Ox.\)
\(y=\sqrt{1-x^{2}}\)

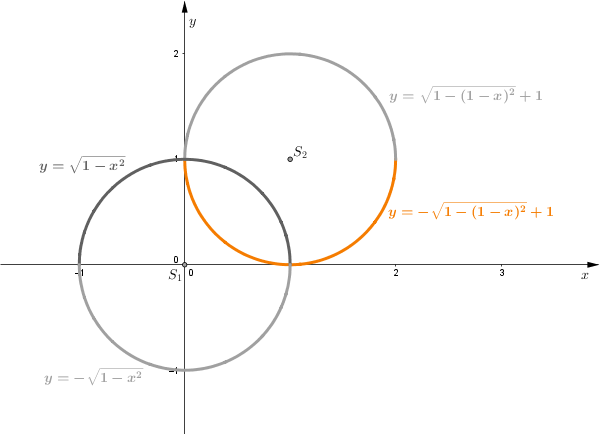
\((x-1)^{2}+(y-1)^{2}=1\\
(y-1)^{2}=1-(x-1)^{2}\\
y-1=\pm \sqrt{1-(x-1)^{2}}\)
Wybieramy ujemny znak pierwiastka, gdyż (przed przesunięciem o 1 jednostkę w górę) interesuje nas ta część okręgu, która znajduje się pod osią \(Ox.\)
\(y=-\sqrt{1-(x-1)^{2}}+1\)

Zatem pole zacieniowanego obszaru wynosi:
\[{\displaystyle |P|=\int_{0}^{1}\left [\sqrt{1-x^{2}}-\left (\sqrt{1-(x-1)^{2}}+1   \right ) \right ]\ dx=\int_{0}^{1}\left [\sqrt{1-x^{2}}+\sqrt{1-(x-1)^{2}}-1  \right ]\ dx=\int_{0}^{1}\sqrt{1-x^{2}}\ dx+\int_{0}^{1} \sqrt{1-(x-1)^{2}}\ dx- \int_{0}^{1} 1\ dx  =\cdots }\]
Dla wygody dzielimy całkę na trzy oddzielne i liczymy osobno, aby wrócić do liczenia pola powierzchni obszaru, tj.
 \({\displaystyle \int_{0}^{1}\sqrt{1-x^{2}}\ dx=}\)

Zatem wracając do pola obszaru \(|P|\) oraz wstawiając wyżej uzyskane całki, otrzymamy:
\[{\displaystyle |P|=\int_{0}^{1}\left [\sqrt{1-x^{2}}-\left (\sqrt{1-(x-1)^{2}}+1   \right ) \right ]\ dx=\int_{0}^{1}\left [\sqrt{1-x^{2}}+\sqrt{1-(x-1)^{2}}-1  \right ]\ dx=\int_{0}^{1}\sqrt{1-x^{2}}\ dx+\int_{0}^{1} \sqrt{1-(x-1)^{2}}\ dx- \int_{0}^{1} 1\ dx  =\frac{\pi}{4}+\frac{\pi}{4}-1=\frac{\pi}{2}-1 }\]

Kardioida - to szczególny przypadek ślimaka Pascala, dla \(l=2r.\)  Kardioida, zwana krzywą sercową, jest opisana przez ustalony punkt okręgu toczącego się bez poślizgu po zewnętrzu innego nieruchomego okręgu o tej samej średnicy.

Wyznaczamy wektor wodzący \(r,\) aby skorzystać ze wzoru na pole obszaru ograniczonego krzywą \(r(\varphi).\)
Do równania \({\displaystyle (x^{2}+y^{2}-2ax)^{2}=4a^{2}(x^{2}+y^{2})}\) podstawiamy współrzędne biegunowe
\(\begin{cases}
x=r \cos \varphi\\
y=r \sin \varphi
\end{cases},\) gdzie \(r \geqslant  0, \ \ \varphi \in \left \langle 0; 2\pi \right \rangle.\)
\[ \begin{array}{l}
{\displaystyle (x^{2}+y^{2}-2ax)^{2}=4a^{2}(x^{2}+y^{2})}\\
{\displaystyle \left (r^{2}\cos^{2}\varphi + r^{2}\sin^{2}\varphi -2ar\cos \varphi  \right )^{2}=4a^{2}\left ( r^{2}\cos^{2}\varphi+r^{2}\sin^{2}\varphi \right )}\\
{\displaystyle \left (r^{2}\cos^{2}\varphi + r^{2}\sin^{2}\varphi -2ar\cos \varphi  \right )^{2}=4a^{2}r^{2}\underbrace{\left ( \cos^{2}\varphi+\sin^{2}\varphi \right )}_{=1}}\\
{\displaystyle \left (r^{2}\cos^{2}\varphi + r^{2}\sin^{2}\varphi -2ar\cos \varphi  \right )^{2}=4a^{2}r^{2}}\\
{\displaystyle r^{2}\cos^{2}\varphi + r^{2}\sin^{2}\varphi -2ar\cos \varphi  =2ar}\\
{\displaystyle r^{2}\underbrace{\left (\cos^{2}\varphi + \sin^{2}\varphi  \right )}_{=1} -2ar\cos \varphi  =2ar}\\
{\displaystyle r^{2}-2ar\cos \varphi  =2ar}\\
{\displaystyle r^{2}-2ar\cos \varphi -2ar=0}\\
{\displaystyle r^{2}-2ar\left (\cos \varphi + 1 \right )=0}\\
{\displaystyle r\left [r-2a\left (\cos \varphi + 1 \right )  \right ]=0}\\
{\displaystyle r=0 \ \ \vee \ \ r=2a\left (\cos \varphi + 1 \right )}
\end{array}\]

Ponieważ dla \(r=0\) krzywa jest punktem \((0,0),\) zatem jej pole jest równe \(0.\)
Obliczymy pole obszaru \({\displaystyle |P|=\frac{1}{2}\int_{\alpha }^{\beta } r^{2}(\varphi )\ d\varphi}\)  ograniczonego krzywą \( r=2a\left (\cos \varphi + 1 \right ),\) dla \(\varphi \in \left \langle 0; 2\pi \right \rangle.\)

\[ \begin{array}{l}
{\displaystyle |P|=\frac{1}{2}\int_{0}^{2\pi} \left [2a\left (\cos \varphi + 1 \right ) \right ]^{2}\ d \varphi=}\\
{\displaystyle = 2a^{2}\int_{0}^{2\pi}\left (\cos \varphi + 1 \right )^{2} \ d \varphi =}\\
{\displaystyle  =2a^{2}\int_{0}^{2\pi}\left (\cos^{2} \varphi + 2\cos \varphi + 1 \right )\ d \varphi=}\\
{\displaystyle = 2a^{2}\int_{0}^{2\pi}\left (\frac{1-\cos 2\varphi}{2} + 2\cos \varphi + 1 \right )\ d \varphi=}\\
{\displaystyle =2a^{2}\int_{0}^{2\pi}\left (\frac{1}{2}-\frac{\cos 2\varphi}{2} + 2\cos \varphi + 1 \right )\ d \varphi=}\\
{\displaystyle = 2a^{2}\int_{0}^{2\pi}\left (\frac{3}{2}-\frac{\cos 2\varphi}{2} + 2\cos \varphi \right )\ d \varphi=}\\
{\displaystyle = 2a^{2} \Big [ \frac{3}{2}\varphi +2 \sin \varphi -\frac{1}{2}\cdot \frac{1}{2}\sin 2\varphi \Big ]_{0}^{2\pi} =}\\
{\displaystyle = 2a^{2}\left ( \frac{3}{2}\cdot 2\pi +2 \sin 2\pi -\frac{1}{4}\sin 4\pi -(0+0-0)  \right ) =}\\
{\displaystyle =2a^{2}\cdot 3 \pi=6a^{2}\pi.}
\end{array}\]

Pierwszy zwój spirali Archimedesa dla \(\varphi \in \left \langle 0; 2\pi \right \rangle\) wygląda następująco.

Stosujemy wzór na  pole obszaru \({\displaystyle |P|=\frac{1}{2}\int_{\alpha }^{\beta } r^{2}(\varphi )\ d\varphi}\)  ograniczonego krzywą opisaną za pomocą współrzędnych biegunowych dla \(\varphi \in \left \langle 0; 2\pi \right \rangle.\)
Zatem
\({\displaystyle |P|=\frac{1}{2}\int_{0}^{2\pi}(a\varphi )^{2}d\varphi= \frac{1}{2}a^{2}\int_{0}^{2\pi}\varphi^{2}d\varphi =\frac{1}{2}a^{2} \Big [ \frac{\varphi^{3}}{3} \Big ]_{0}^{2\pi}= \frac{1}{2}a^{2} \left [ \frac{(2\pi)^{3}}{3}-0 \right ]=\frac{1}{2}a^{2}\cdot \frac{8\pi^{3}}{3}=\frac{4\pi^{3}a^{2}}{3}.}\)

Krzywa przedstawiona parametrycznie \(\left\{\begin{matrix}
x(t)=a(t-\sin t)\\
y(t)=a(1-\cos t)
\end{matrix}\right.,\) dla \(t\in \left \langle 0; 2\pi \right \rangle\) to cykloida. Cykloidę zakreśla punkt leżący na obwodzie koła, które toczy się bez poślizgu po prostej.

Pole cykloidy dla \(t\in \left \langle 0; 2\pi \right \rangle\) to pole obszaru między pojedynczym fragmentem cykloidy oraz osią \(Ox.\) Liczymy pole obszaru \({\displaystyle |P|=\int_{t_{1}}^{t_{2}}\left | y(t)\cdot x'(t) \right |\ dt}\)  ograniczonego krzywą opisaną parametrycznie.
\[ \begin{array}{l}
{\displaystyle |P|=\int_{0}^{2\pi}a(1-\cos t)\cdot a (1-\cos t) dt=}
{\displaystyle a^{2}\int_{0}^{2\pi}(1-\cos t)^{2}dt=}\\
{\displaystyle = a^{2}\int_{0}^{2\pi}(1-2\cos t+\color{#F57C00}{\cos^{2} t})dt=}
{\displaystyle  a^{2}\int_{0}^{2\pi}\left (1-2\cos t+\frac{1}{2}\cos 2t+\frac{1}{2}  \right )dt=}\\
{\displaystyle =a^{2}\int_{0}^{2\pi}\left (\frac{3}{2}-2\cos t+\frac{1}{2}\cos 2t  \right )dt= }
{\displaystyle a^{2}\Big [\frac{3}{2}t-2\sin t+\frac{1}{4}\sin 2t \Big ]_{0}^{2\pi}=}\\
{\displaystyle =a^{2}\Big [\frac{3}{2}\cdot 2\pi-2\sin 2\pi+\frac{1}{4}\sin 2\cdot 2\pi -(0-0+0) \Big ]=}
{\displaystyle a^{2}\cdot 3 \pi=3\pi a^{2}.}
\end{array}\]
\(\cos^{2}t\) \({\displaystyle \cos 2t=\cos^{2}t-\sin^{2}t}\\ {\displaystyle \cos 2t=\cos^{2}t-\left (1-\cos^{2}t \right )}\\ {\displaystyle \cos 2t=\cos^{2}t-1+\cos^{2}t }\\ {\displaystyle \cos 2t=2\cos^{2}t-1}\\ {\displaystyle \cos 2t + 1=2\cos^{2}t}\\ {\displaystyle \cos^{2}t}=\frac{\cos 2t + 1}{2}\)