Zadanie 3.2.1
  1. Analiza matematyczna 1
  2. 3. Funkcje
  3. 3.2 Funkcja liniowa i kwadratowa
  4. Zadanie 3.2.1

 Ćwiczenie interaktywne

Zadaniem jest przedstawienie wzoru funkcji liniowej w postaci kanonicznej, wyznaczenie dwóch punktów, przez które przechodzi dana prosta \(l\) i przesunięcie narysowanej prostej tak, aby otrzymać prostą \(l.\)

 Polecenie

Mając daną funkcję liniową wyznacz:
  1. współczynnik kierunkowy \(a\) i wyraz wolny \(b,\)
  2. dziedzinę i zbiór wartości funkcji,
  3. miejsce zerowe,
  4. monotoniczność,
  5. zbiory argumentów, dla których funkcja przyjmuje wartości ujemne i dodatnie,
  6. punkty przecięcia wykresu funkcji z osiami układu współrzędnych,
  7. wartość funkcji dla argumentu \(x=-3,\)
  8. argument, dla którego funkcja przyjmuje wartość \(4\),
oraz naszkicuj wykres funkcji.

 Wskazówki

Definicja funkcji liniowej

Funkcją liniową nazywamy funkcję określoną na zbiorze liczb rzeczywistych, daną wzorem \( f(x)=ax+b\) lub \(y=ax+b,\) gdzie \(a,b \in \mathbb{R}.\)

  • Wykresem funkcji liniowej jest prosta.
  • Jest to postać kierunkowa, w której \(a\) nazywamy współczynnikiem kierunkowym prostej, \(b\) wyrazem wolnym.
Każdą prostą daną w postaci kierunkowej można zapisać w postaci ogólnej.
Postacią ogólną równania prostej nazywamy równanie \(Ax+By+C=0 ,\) gdzie \(A\) i \(B\) nie są jednocześnie równe zero. Warunek ten jest spełniony, gdy \(A^{2}+B^{2}>0. \)
Rysunek 3.2.1

Własności funkcji liniowej

  1. Dziedziną funkcji liniowej jest zbiór liczb rzeczywistych \(\mathbb{R}\).
  2. Zbiorem wartości funkcji liniowej jest zbiór liczb rzeczywistych lub zbiór \(\left \{ c \right \}\) w przypadku funkcji stałej \(f(x)=c,\) (gdzie \(c\) jest pewną liczbą należącą do zbioru liczb rzeczywistych).
  3. Miejsca zerowe:
    • Jedno miejsce zerowe: \(x_{0}=-\displaystyle\frac{b}{a}\) dla \(a\neq0,\)
    • brak miejsc zerowych, jeśli \(a=0 \wedge  b\neq 0\)  (funkcja stała, różna od \(y=0\),)
    • nieskończenie wiele miejsc zerowych, jeśli \(a=0 \wedge  b=0\) (funkcja stała \(y=0.\))
  4. Monotoniczność:
    • funkcja jest rosnąca, jeśli \(a>0,\)
    • funkcja malejąca dla \(a<0,\)
    • stała, jeśli \(a=0.\)
  5. Punkty przecięcia z osiami układu współrzędnych:
    • z osią \(OX\): \(\left ( -\displaystyle\frac{b}{a},0 \right ),\)
    • z osią \(OY\): \((0,b).\)

 Funkcja 1

\(2x-y+4=0\)

 Rozwiązanie

1. Aby wyznaczyć współczynnik kierunkowy i wyraz wolny musimy mieć równanie funkcji liniowej w postaci kierunkowej. (Wyznaczamy niewiadomą \(y\) z równania \(2x-y+4=0.\))
\[ \begin{array}{l}2x-y+4=0\\
-y=-2x-4\\
-y=-2x-4 \quad /\cdot (-1)\\
y=2x+4.\end{array}\]
Zatem \(a=2\) oraz \(b=4.\)
2. Dziedziną funkcji liniowej \(y=2x+4\) jest zbiór liczb rzeczywistych. Ponieważ nie jest to funkcja stała zbiorem wartości jest również zbiór liczb rzeczywistych. Symbolicznie \(D=\mathbb{R}, ZW=\mathbb{R}.\)
3. Wyznaczając miejsce zerowe możemy skorzystać z gotowego wzoru \(x_{0}=-\displaystyle\frac{b}{a}\) lub szukać argumentu, dla którego funkcja przyjmuje wartość \(0.\)
Szukamy takiego argumentu przyrównując wartość \(2x+4\) do zera.
\[2x+4=0\\2x=-4\\x=-2.\] Zatem \(x_{0}=-2.\)
4. Ponieważ współczynnik kierunkowy \(a=2>0,\) zatem funkcja jest rosnąca na całej dziedzinie.
5. Zbiory argumentów, dla których funkcja przyjmuje wartości dodatnie lub ujemne wyznaczamy rozwiązując nierówności \(2x+4>0\) oraz \(2x+4<0.\)
\[2x+4>0,\quad\quad 2x+4<0\\2x>-4 \quad\quad\quad 2x<-4\\x>-2\quad\quad\quad x<-2.\] Zatem
\[f(x)>0 \Leftrightarrow x\in \left ( -2;\infty  \right )\\
f(x)<0 \Leftrightarrow x\in \left (-\infty;-2  \right ).\]
6.
Punkt przecięcia z osią \(OX\) to punkt \( (x_{0}, 0),\) czyli punkt \( (-2,0).\)
Punkt przecięcia z osią \(OY\) to punkt \((0,b),\) czyli punkt \( (0,4).\)
7. \( f(-3)=2\cdot (-3)+4=-6+4=-2.\)
8. Argument, dla którego wartość wynosi \(4\), wyznaczamy przyrównując \(2x+4\) do \(4.\)
Zatem \[2x+4=4\\2x=4-4\\2x=0\\x=0.\]
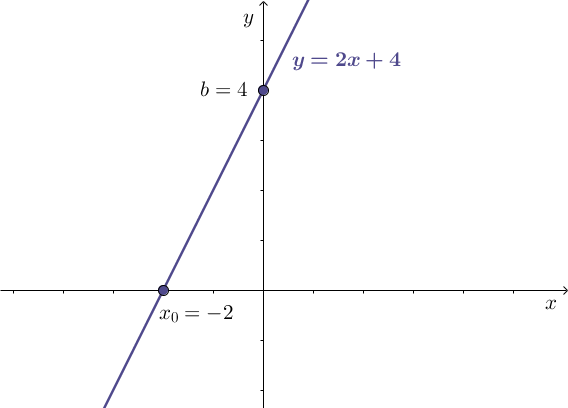
9. Aby naszkicować wykres funkcji liniowej \(y=2x+4\) wystarczy zaznaczyć w układzie współrzędnych dwa punkty należące do tej prostej.
Takimi punktami są na przykład punkty przecięcia z osiami układu współrzędnych (pkt.6 rozwiązania zadania).
Zaznaczamy te punkty i prowadzimy przez nie prostą.
Rysunek.3.2.2

 Odpowiedź

  1. \(a=2, b=4\)
  2. \(D=\mathbb{R}, ZW=\mathbb{R}\)
  3. \(x_{0}=-2\)
  4. Funkcja rosnąca na \(D\)
  5. \(f(x)>0 \Leftrightarrow x\in \left ( -2;\infty  \right )\\
    f(x)<0 \Leftrightarrow x\in \left (-\infty;-2  \right )\)
  6. \( (-2,0), (0,4)\)
  7. \(f(-3)=-2\)
  8. \(x=0\)

 Funkcja 2

\(x-y=0\)

 Rozwiązanie

Uwaga
Rozwiązując to ćwiczenie w dziewięciu krokach masz do wyboru w każdym z nich trzy możliwości. Wybór prawidłowej odpowiedzi odkryje kolejny krok rozwiązania zadania.

 Krok 1

Wyznaczając współczynnik kierunkowy \(a\) oraz wyraz wolny \(b\) dostaniemy:

\[a=1\\b=1\]

Odpowiedź nieprawidłowa

\[a=1\\b=0\]

Odpowiedź prawidłowa

\[a=0\\b=0\]

Odpowiedź nieprawidłowa

 Krok 2

Dziedzina i zbiór wartości danej funkcji liniowej wynoszą:

\[D=\mathbb{R}\\ZW=\left \{ 1 \right \}\]

Odpowiedź nieprawidłowa

\[D=\mathbb{R}\\ZW=\mathbb{R}\]

Odpowiedź prawidłowa

\[D=\left \{ 1 \right \}\\ZW=\mathbb{R}\]

Odpowiedź nierpawidłowa

 Krok 3

Miejscem zerowym funkcji liniowej \(f(x)=x\) jest:

\(x_{0}=-1\)

Odpowiedź nieprawidłowa

\(x_{0}=1\)

Odpowiedź nierpawidłowa

\(x_{0}=0\)

Odpowiedź prawidłowa

 Krok 4

Monotoniczność funkcji \(f\) opisuje odpowiedź:

Funkcja jest rosnąca na \(\mathbb{R}\)

Odpowiedź prawidłowa

Funkcja jest malejąca na \(\mathbb{R}\)

Odpowiedź nieprawidłowa

Funkcja jest stała na \(\mathbb{R}\)

Odpowiedź nierpawidłowa

 Krok 5

Zbiorami argumentów, dla których funkcja \(f\) przyjmuje wartości dodatnie i ujemne są:

\(f(x)>0 \Leftrightarrow  x\in (0;\infty )\\
f(x)<0 \Leftrightarrow  x\in (-\infty;0 )\)

Odpowiedź prawidłowa

\(f(x)>0 \Leftrightarrow  x\in (1;\infty )\\
f(x)<0 \Leftrightarrow  x\in (-\infty;1 )\)

Odpowiedź nierpawidłowa

\(f(x)>0 \Leftrightarrow  x\in (-1;\infty )\\
f(x)<0 \Leftrightarrow  x\in (-\infty;-1 )\)

Odpowiedź nierpawidłowa

 Krok 6

Punktami przecięcia się wykresu funkcji \(f(x)=x\) z osiami układu współrzędnych są:

Z osią \(OX\): \((1,0),\)
z osią \(OY\): \((0,1).\)

Odpowiedź nieprawidłowa

Z osią \(OX\): \((-1,0),\)
z osią \(OY\): \((0,-1).\)

Odpowiedź nierpawidłowa

Z osiami \(OX\) i \(OY\): \((0,0),\)

Odpowiedź prawidłowa

 Krok 7

Wartość funkcji dla argumentu \(x=-3\) wynosi:

\(f(-3)=0\)

Odpowiedź nieprawidłowa

\(f(-3)=-1\)

Odpowiedź nieprawidłowa

\(f(-3)=-3\)

Odpwiedź prawidłowa

 Krok 8

Argumentem, dla którego funkcja \(f\) przyjmuje wartość \(4\) jest:

\(f(x)=4 \Leftrightarrow x=4\)

Odpowiedź prawidłowa

\(f(x)=4 \Leftrightarrow x=0\)

Odpwiedź nieprawidłowa

\(f(x)=4 \Leftrightarrow x=-4\)

Odpowiedź nieprawidłowa

 Krok 9

Wykresem funkcji \(f(x)=x\) jest:

Rysunek 3.2.2_1

Odpowiedź prawidłowa

Rysunek 3.2.2_2

Odpowiedź nieprawidłowa

Rysunek 3.2.2_3

Odpowiedź nierpawidłowa

 Podsumowanie

Wszystkie kroki zadania 3.2.1.2 zostały wykonane prawidłowo.

 Funkcja 3

\(x-2y=6\)

 Rozwiązanie

Uwaga
W każdym z pytań wpisz odpowiedź i sprawdź poprawność przyciskiem "Sprawdź".

1.

Współczynnik kierunkowy prostej \(x-2y=6\) wynosi:

a =

2.

Wyraz wolny funkcji \(x-2y=6\) wynosi:

b =

3.

Dziedziną i zbiorem wartości funkcji \(f\) jest zbiór:

4.

Miejsce zerowe funkcji \(f\) wynosi:

\(x_{0}=\)

5.

Funkcja \(f\) jest:

6.

Zaznacz wszystkie prawidłowe odpowiedzi

7.

Wartość funkcji \(f\) dla argumentu \(-3\) wynosi:

\(f(-3)=\)

8.

Funkcja \(f\) przyjmuje wartość \(4\) dla argumentu:

\(x=\)

9.

Wykresem funkcji liniowej \(f\) jest:

Podsumowanie rozwiązań zadania

1.
\[ \begin{array}{l}
x-2y=6\\
-2y=-x+6\\
y=\displaystyle\frac{1}{2}x-3\\
a=\displaystyle\frac{1}{2}.
\end{array}\]
2.
\[b=-3\]
3.
\[ \begin{array}{l}
D=\mathbb{R}\\
ZW=\mathbb{R}
\end{array}\]
4.
\[ \begin{array}{l}
f(x)=0\\
\displaystyle\frac{1}{2}x-3=0\\
\displaystyle\frac{1}{2}x=3\\
x_{0}=6
\end{array}\]
5.
\[ a=\displaystyle\frac{1}{2} \gt 0 \ \Leftrightarrow \ f \nearrow \]
6.
\[ \begin{array}{l}
f(x) \gt 0 \ \Leftrightarrow \ x\in \left ( 6;\infty  \right )\\
f(x) \lt 0 \ \Leftrightarrow \ x\in \left ( -\infty;6  \right )
\end{array}\]
7.
\[f(-3)=\displaystyle\frac{1}{2}(-3)-3=-\displaystyle\frac{3}{2}-3=-4,5\]
8.
\[ \begin{array}{l}
f(x)=4\\
\displaystyle\frac{1}{2}x-3=4\\
\displaystyle\frac{1}{2}x=7\\
x=14
\end{array}\]
9. Wykres funkcji \(y=\displaystyle\frac{1}{2}x-3.\)
Rysunek 3.2.3_1

 Polecenie

Mając daną funkcję liniową wyznacz:
  1. współczynnik kierunkowy \(a\) i wyraz wolny \(b,\)
  2. dziedzinę i zbiór wartości funkcji,
  3. miejsce zerowe,
  4. monotoniczność,
  5. zbiory argumentów, dla których funkcja przyjmuje wartości ujemne i dodatnie,
  6. punkty przecięcia wykresu funkcji z osiami układu współrzędnych,
  7. wartość funkcji dla argumentu \(x=-3,\)
  8. argument, dla którego funkcja przyjmuje wartość \(4\),
oraz naszkicuj wykres funkcji.

 Funkcja 1

\(3x+y-1=0\)

 Odpowiedź

1. \(a=-3, b=1,\)
2. \(D=\mathbb{R}, ZW=\mathbb{R},\)
3. \(x_{0}=\displaystyle\frac{1}{3},\)
4. funkcja malejąca,
5. \(f(x) \gt 0 \Leftrightarrow x\in (-\infty ;\displaystyle\frac{1}{3}),\\
f(x) \lt 0 \Leftrightarrow x\in (\displaystyle\frac{1}{3}; \infty),\)
6. Punkt przecięcia z osią \(OX\): \((\displaystyle\frac{1}{3},0),\) z osią \(OY\): \((0;1),\)
7. \(f(-3)=10,\)
8. \(f(x)=4 \Leftrightarrow x=-1.\)
9. Wykres funkcji \(y=-3x+1\)
Rysunek 3.2.spr.1

 Rozwiązanie

3. \(-3x+1=0\\-3x=-1\\x=\displaystyle\frac{1}{3}.\)
5. \(-3x+1>0\\-3x>-1\\ x<\displaystyle\frac{1}{3}.\)
7. \(f(-3)=-3(-3)+1=9+1=10.\)
8. \(f(x)=4\\-3x+1=4\\-3x=4-1\\-3x=3\\x=-1.\)

 Funkcja 2

\(y=2\)

 Odpowiedź

1. \(a=0, b=2\)
2.\(D=\mathbb{R}, ZW=\mathbb{R}\)
3. brak miejsc zerowych
4. funkcja stała
5. \(\underset{x\in\mathbb{R}}{\huge\forall } f(x)>0\)
6. Punkt przecięcia z osią \(OX\) - nie istnieje , z osią \(OY\): \((0,2)\)
7. \(f(-3)=2\)
8. nie istnieje
9.Wykres funkcji \(y=2\)
Rysunek 3.2.spr.2

 Funkcja 3

\(x-2y=5\)

 Odpowiedź

Funkcja ma postać kanoniczną \(y=\displaystyle\frac{1}{2}x-\displaystyle\frac{5}{2}.\)
1. \(a=(\displaystyle\frac{1}{2}, -\displaystyle\frac{5}{2})\)
2. \(D=\mathbb{R}, ZW=\mathbb{R}\)
3. \(x_{0}=5\)
4. funkcja rosnąca
5. \(f(x) \gt 0 \Leftrightarrow x\in (5;\infty )\\ f(x) \lt 0 \Leftrightarrow x\in (-\infty;5 )\)
6. Punkt przecięcia z osią \( OX: \ (5,0),\) z osią \( OY: \ (0,-\displaystyle\frac{5}{2})\)
7. \(f(-3)=\displaystyle\frac{1}{2}\cdot (-3)-\displaystyle\frac{5}{2}=-\displaystyle\frac{8}{2}=-4\)
8. \(\displaystyle\frac{1}{2}x-\displaystyle\frac{5}{2}=4\\x-5=8\\x=8+5\\x=13\)
9. Wykres funkcji \(y=\displaystyle\frac{1}{2}x-\displaystyle\frac{5}{2}\)
Rysunek 3.2.spr.3