Dla \(\alpha=\displaystyle\frac{1}{k}\ ,\) gdzie \(k \in \left \{ -2,-4,-6 \cdots \right \}\)
Wykres funkcji potęgowej \(f(x)=x^{\alpha },\) dla \(\alpha=\displaystyle\frac{1}{k}\ ,\) gdzie \(k \in \left \{ -2,-4,-6 \cdots \right \}.\)
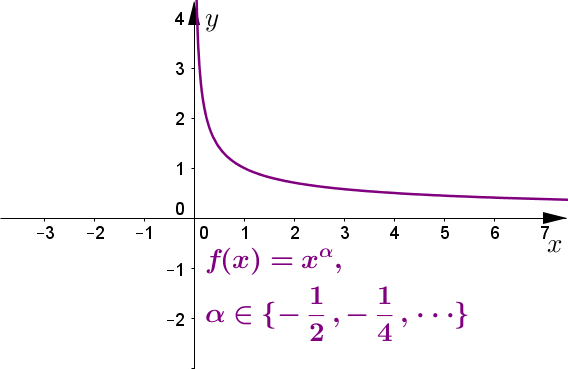
\(D=\mathbb{R}\setminus \left \{ 0 \right \}\)
\(ZW=\mathbb{R}\setminus \left \{ 0 \right \}\)
\(f \searrow \ \ \Leftrightarrow \ \ x\in \left ( -\infty;0 \right )\cup \left ( 0;\infty \right ) \)
Brak miejsc zerowych.
\(f(x) \gt 0 \ \Leftrightarrow \ x\in \left ( 0;\infty \right )\)
\(f(x) \lt 0 \ \Leftrightarrow \ x\in \left ( -\infty ; 0 \right )\)
Asymptoty: \(x=0, \ \ y=0.\)

